如何绘制和理解反正切函数（Arctan）的图像及其特征？

在数学的浩瀚宇宙中，隐藏着无数既神秘又迷人的函数图像，它们如同夜空中最亮的星，引领着探索者一步步深入未知的领域。今天，就让我们携手踏上一段奇妙的旅程，去揭开一位低调而优雅的明星——反正切函数（Arctangent Function，通常表示为arctan(x)或tan^(-1)(x)）图像的面纱。这不仅仅是一场数学公式的解析，更是一次心灵与几何美学的邂逅。

初探秘境：何为反正切函数？

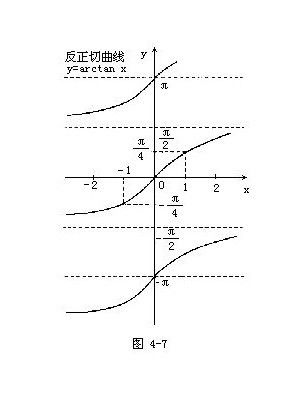
想象一下，你站在一座古老而庄严的图书馆前，手中的是一本尘封已久的数学典籍。翻开它，一行行公式跃然纸上，其中，arctan(x)这个看似简单的符号，却蕴含着无限的可能。简单来说，反正切函数是三角函数中正切函数的反函数。正切函数tan(θ)告诉我们，在直角三角形中，对边与邻边的比值是多少；而反正切函数则反其道而行之，它询问：“如果某个比值（即tan值）是x，那么对应的角度θ是多少？”这里的θ值，就是arctan(x)的结果，且由于角度的限制，其值域通常定义在-π/2到π/2之间（或等价地，在-90°到90°之间）。

走进图像：绘制与解析

现在，让我们拿起画笔，在心灵的画布上勾勒出arctan(x)的图像。这是一条怎样的曲线呢？它以一种温柔而坚定的姿态，自左下角出发，缓缓上升，直至右上角，形成了一条光滑无间断的曲线。这条曲线，就像是自然界中蜿蜒流淌的小溪，虽不壮阔，却细腻入微，引人深思。

起点与终点：arctan(x)的图像在x轴上的两个渐近线处接近但永不触及，这两点分别是x→-∞时趋近于-π/2（或-90°），以及x→+∞时趋近于π/2（或90°）。这种特性使得图像在视觉上呈现出一种“开放但有限”的美感，仿佛是对无限可能的一种优雅诠释。

中心对称：仔细观察，你会发现arctan(x)的图像关于原点(0,0)中心对称。这意味着，如果点(a,b)在图像上，那么点(-a,-b)也必然在图像上。这种对称性，不仅让图像看起来更加和谐统一，也揭示了反正切函数在数学上的某种内在规律。

单调递增：在整个定义域内，arctan(x)是单调递增的。这意味着，随着x值的增大，arctan(x)的值也在逐渐增大，但增速逐渐放缓。这种特性，让图像呈现出一种平缓上升的趋势，如同日出时分的天边，温柔而充满希望。

深度探索：应用场景与美学价值

然而，反正切函数的魅力远不止于此。它不仅是数学殿堂中的一枚瑰宝，更在实际应用中发挥着重要作用。从工程学到经济学，从物理学到计算机科学，反正切函数的身影无处不在。例如，在信号处理中，它常用于相位角的计算；在机器人学中，帮助计算关节的角度；甚至在金融领域，也能见到它作为某种转换函数的身影。

而当我们从实用主义的视角跳出，转而关注其美学价值时，会发现arctan(x)的图像本身就是一种美的表达。它的流畅、对称与和谐，让人联想到自然界的种种美景：山峦的起伏、河流的蜿蜒、云彩的飘逸……这些自然界的形态，在某种抽象的意义上，与反正切函数的图像产生了共鸣。

结语：一场心灵的旅行

至此，我们的旅程即将结束。但请相信，每一次与数学的相遇，都是一次心灵的洗礼和智慧的启迪。反正切函数图像的美，不仅仅在于它本身的几何特性，更在于它背后所蕴含的数学思想、实际应用以及与人类文明的深刻联系。让我们带着这份感悟，继续在数学的世界里遨游，探索更多未知的奥秘，感受那份属于数学独有的魅力与力量。

在未来的日子里，不妨时常回想起这段关于反正切函数图像的旅程，或许在某个不经意的瞬间，它会成为你解决问题时的一束灵光，或是你心灵深处的一份宁静与慰藉。