arc三角函数的导数分别是什么？

在微积分学中，三角函数的导数占据着举足轻重的地位。其中，“arc”前缀通常指的是反三角函数，也称为反三角函数或逆三角函数。这些函数包括反正弦（arcsin）、反余弦（arccos）、反正切（arctan）、反余切（arccot）、反正割（arcsec）和反余割（arccsc）。了解这些反三角函数的导数不仅有助于深入理解微积分的基本原理，还在工程、物理和数学等多个领域有着广泛的应用。

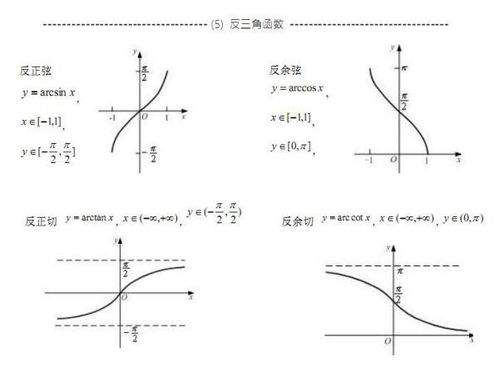
首先，让我们回顾一下基本的三角函数：正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc）。这些函数在直角三角形中定义，描述了角度与边长之间的关系。反三角函数则是这些函数的逆运算，即给定一个函数值，反三角函数能够求出对应的角度。

反正弦函数（arcsin）的导数

反正弦函数定义为y = arcsin(x)，其导数可以通过隐函数求导法得到。设y = arcsin(x)，则有x = sin(y)。对两边同时求导，得到1 = cos(y) * dy/dx。由于cos(y) = √(1 - sin²(y)) = √(1 - x²)，因此dy/dx = 1/√(1 - x²)。所以，反正弦函数的导数为：

(d/dx)arcsin(x) = 1/√(1 - x²)

反余弦函数（arccos）的导数

反余弦函数定义为y = arccos(x)，其求导过程与反正弦函数类似。设y = arccos(x)，则有x = cos(y)。对两边同时求导，得到1 = -sin(y) * dy/dx。由于sin(y) = √(1 - cos²(y)) = √(1 - x²)，且注意负号，因此dy/dx = -1/√(1 - x²)。所以，反余弦函数的导数为：

(d/dx)arccos(x) = -1/√(1 - x²)

反正切函数（arctan）的导数

反正切函数定义为y = arctan(x)，其导数同样可以通过隐函数求导法得到。设y = arctan(x)，则有x = tan(y)。对两边同时求导，得到1 = (1/cos²(y)) * dy/dx = sec²(y) * dy/dx。由于sec²(y) = 1 + tan²(y) = 1 + x²，因此dy/dx = 1/(1 + x²)。所以，反正切函数的导数为：

(d/dx)arctan(x) = 1/(1 + x²)

反余切函数（arccot）的导数

反余切函数定义为y = arccot(x)，其求导过程与反正切函数类似。设y = arccot(x)，则有x = cot(y)。对两边同时求导，得到1 = -(1/sin²(y)) * dy/dx = -csc²(y) * dy/dx。由于csc²(y) = 1 + cot²(y) = 1 + x²，且注意负号，因此dy/dx = -1/(1 + x²)。所以，反余切函数的导数为：

(d/dx)arccot(x) = -1/(1 + x²)

反正割函数（arcsec）和反余割函数（arccsc）的导数

对于反正割函数y = arcsec(x)和反余割函数y = arccsc(x)，它们的导数求解过程相对复杂，但同样基于隐函数求导法。

对于反正割函数，设y = arcsec(x)，则有x = sec(y)。对两边同时求导，得到1 = sec(y)tan(y) * dy/dx。由于sec(y) = x且tan(y) = √(sec²(y) - 1) = √(x² - 1)，因此dy/dx = 1/(x√(x² - 1))。所以，反正割函数的导数为：

(d/dx)arcsec(x) = 1/(x√(x² - 1))

对于反余割函数，设y = arccsc(x)，则有x = csc(y)。对两边同时求导，得到1 = -csc(y)cot(y) * dy/dx。由于csc(y) = x且cot(y) = 1/tan(y) = √(csc²(y) - 1) = √(x² - 1)/x，因此dy/dx = -1/(x√(x² - 1))。所以，反余割函数的导数为：

(d/dx)arccsc(x) = -1/(x√(x² - 1))

应用与重要性

反三角函数的导数在微积分学中有着广泛的应用。例如，在求解涉及反三角函数的复合函数的导数时，需要用到这些导数公式。此外，在物理学和工程学领域，反三角函数及其导数常用于描述周期现象、波动和振动等问题。

在物理学中，反三角函数常用于描述角度和位移之间的关系，如摆动的钟摆、振动的弹簧等。在工程学中，反三角函数及其导数则用于计算结构的应力、应变和位移等参数。

结论

综上所述，反三角函数的导数在微积分学中占据着重要的地位。通过隐函数求导法，我们可以得到这些函数的导数公式。这些公式不仅有助于深入理解微积分的基本原理，还在物理学、工程学等多个领域有着广泛的应用。因此，掌握反三角函数的导数对于学习和应用微积分学至关重要。

通过本文的介绍，我们详细阐述了反正弦、反余弦、反正切、反余切、反正割和反余割等反三角函数的导数公式及其推导过程。同时，我们也强调了这些导数在微积分学和实际应用中的重要性。希望本文能够帮助读者更好地理解和掌握反三角函数的导数知识。