在探讨如何绘制自然对数函数$lnx$的绝对值图像时,我们首先需要理解两个核心概念:自然对数函数$lnx$本身的性质,以及绝对值函数如何影响这些性质。自然对数函数,作为数学分析中的基础工具,其图像展现了一系列独特的特征,如定义域为$(0, +\infty)$,值域为$(-\infty, +\infty)$,且当$x$趋近于0时,$lnx$趋近于负无穷;而当$x$趋近于正无穷时,$lnx$则缓慢增加。
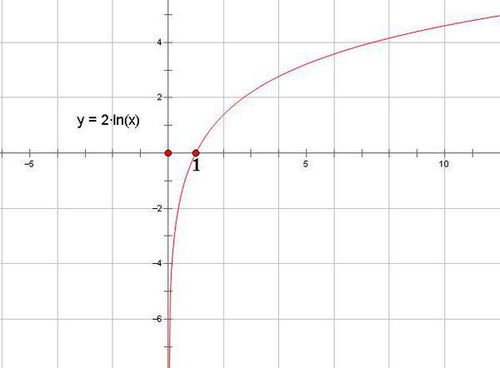
自然对数函数$lnx$的图像是一个经典的“S”型曲线,它穿过点$(1,0)$,并在该点附近呈现出较为平缓的变化趋势。随着$x$的增大,曲线逐渐上升,但增速逐渐放缓,反映了自然增长的概念。此外,该图像在$x$轴上方无限延伸,而在$x$轴下方则没有定义,因为对于任何非正数,自然对数都是未定义的。
绝对值函数,记作$|x|$,是一个将数轴上每一点映射到其非负距离的函数。当应用于函数$f(x)$时,$|f(x)|$表示$f(x)$与$x$轴之间的垂直距离,不考虑方向。因此,绘制$|lnx|$的图像,就是要在保持$lnx$在$x$轴上方特性的同时,将其在$x$轴下方的部分“翻折”到上方,使得整个图像关于$x$轴对称。
1. 绘制基础曲线:首先,绘制出自然对数函数$lnx$在定义域$(0, +\infty)$内的图像。这通常涉及到选择一系列的点(如$x=1, e, e^2, e^3, \ldots$)计算对应的$lnx$值,并将这些点连接成平滑的曲线。
2. 确定翻折点:对于$lnx$来说,其图像始终位于$x$轴上方,因此没有直接的“翻折点”存在于原始图像中。但在考虑绝对值后,我们需要意识到,虽然$lnx$本身不穿越$x$轴,但在绘制$|lnx|$时,我们实际上是在“虚拟地”考虑了它如果在$x$轴下方会如何,并将这部分“反射”到上方。不过,实际操作中,我们只需关注保持$lnx$原有图像不变即可,因为绝对值在这里只涉及“保留正数”和“翻转负数”(但$lnx$没有负数部分)。
3. 完成图像:由于$lnx$的定义域限制和绝对值的特性,绘制$|lnx|$的图像实际上就是绘制$lnx$在其定义域上的图像,无需进行任何实际的“翻转”操作。因此,最终得到的$|lnx|$图像就是$lnx$的图像本身,它完全位于$x$轴上方,且随着$x$的增大而无限上升,但增速逐渐减缓。
定义域:在绘制$|lnx|$时,要特别注意其定义域仍然是$(0, +\infty)$,因为自然对数函数对于非正数没有定义。
图像特征:虽然引入了绝对值概念,但$|lnx|$的图像与$lnx$的图像在视觉上完全一致,这是因为$lnx$的输出始终为正(或0,在$x=1$时)。
实际应用:了解$|lnx|$的图像有助于我们理解某些物理、经济或工程问题中涉及的增长率、衰减率等概念,特别是当这些过程需要被量化为与时间的对数关系时。
综上所述,绘制$|lnx|$的图像实际上是一个理解并应用自然对数函数及其与绝对值函数关系的过程。通过这个过程,我们不仅能加深对这两个函数性质的理解,还能提升解决相关问题时的直观性和准确性。
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2