二进制与十六进制相互转换方法

二进制数与十六进制数之间如何互相转换

在计算机科学中，二进制和十六进制是两种非常重要的数制。二进制是计算机内部处理数据的基础，因为它只有两个数字（0和1），非常适合于电子电路中的高低电平表示。而十六进制则因为其表达简洁，便于人类阅读和编写，常被用作编程中的内存地址和机器码等的表示。那么，二进制数与十六进制数之间是如何互相转换的呢？本文将详细讲解这一转换过程。

二进制转十六进制

方法一：直接转换法

直接转换法是将二进制数从右到左每四位一组进行划分（如果不足四位，则在前面补0），然后将每组二进制数转换为对应的十六进制数。

例如，二进制数 `1101011010` 转换为十六进制数的过程如下：

1. 将二进制数从右到左每四位一组划分，得到 `0011 0101 1010`。

2. 将每组二进制数转换为对应的十六进制数：

`0011` 转换为 `3`

`0101` 转换为 `5`

`1010` 转换为 `A`

3. 将转换后的十六进制数组合起来，得到 `35A`。

方法二：先转十进制再转十六进制

另一种方法是将二进制数先转换为十进制数，然后再将十进制数转换为十六进制数。

例如，二进制数 `1101` 转换为十六进制数的过程如下：

1. 将二进制数 `1101` 转换为十进制数：

`1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 8 + 4 + 0 + 1 = 13`

2. 将十进制数 `13` 转换为十六进制数：

`13` 的十六进制表示为 `D`

这种方法虽然步骤较多，但在处理较大的二进制数时，有时候反而更直观一些。

十六进制转二进制

方法一：逐位转换法

逐位转换法是将十六进制数的每一位分别转换为对应的四位二进制数。

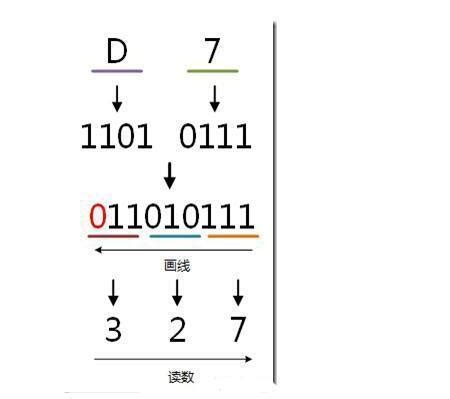
例如，十六进制数 `3A7` 转换为二进制数的过程如下：

1. 将十六进制数 `3A7` 的每一位分别转换为对应的四位二进制数：

`3` 转换为 `0011`

`A`（即10）转换为 `1010`

`7` 转换为 `0111`

2. 将转换后的二进制数组合起来，得到 `0011 1010 0111`。

3. 去掉前导零，得到 `1110100111`。

方法二：先转十进制再转二进制

另一种方法是将十六进制数先转换为十进制数，然后再将十进制数转换为二进制数。

例如，十六进制数 `1A3` 转换为二进制数的过程如下：

1. 将十六进制数 `1A3` 转换为十进制数：

`1 * 16^2 + A（即10） * 16^1 + 3 * 16^0 = 256 + 160 + 3 = 419`

2. 将十进制数 `419` 转换为二进制数：

除2取余法：`419 ÷ 2 = 209 余 1`，`209 ÷ 2 = 104 余 1`，`104 ÷ 2 = 52 余 0`，`52 ÷ 2 = 26 余 0`，`26 ÷ 2 = 13 余 0`，`13 ÷ 2 = 6 余 1`，`6 ÷ 2 = 3 余 0`，`3 ÷ 2 = 1 余 1`，`1 ÷ 2 = 0 余 1`

将余数从下到上排列，得到 `110100011`

这种方法虽然步骤繁琐，但适用于任何进制之间的转换，并且对于理解数制转换的原理很有帮助。

实用技巧与注意事项

1. 8421法：在将二进制转换为十六进制时，可以采用8421法（即4位二进制数的权分别为8、4、2、1），这样可以快速进行转换。

2. 记忆常用转换表：为了提高转换效率，可以记忆一些常用的二进制与十六进制之间的转换表。

3. 补零与去零