十六进制(Hexadecimal),作为计算机领域中广泛使用的一种数制,以其独特的表示方式和便捷的计算特性,在数字编码、内存地址表示及颜色值描述等方面发挥着重要作用。了解并掌握十六进制与其他数制(特别是十进制和二进制)之间的转换方法,对于深入学习计算机科学、编程以及进行数据分析至关重要。本文将从十六进制的基本概念、与十进制和二进制的转换方法以及实际应用等多个维度,详细介绍十六进制转换的相关知识。
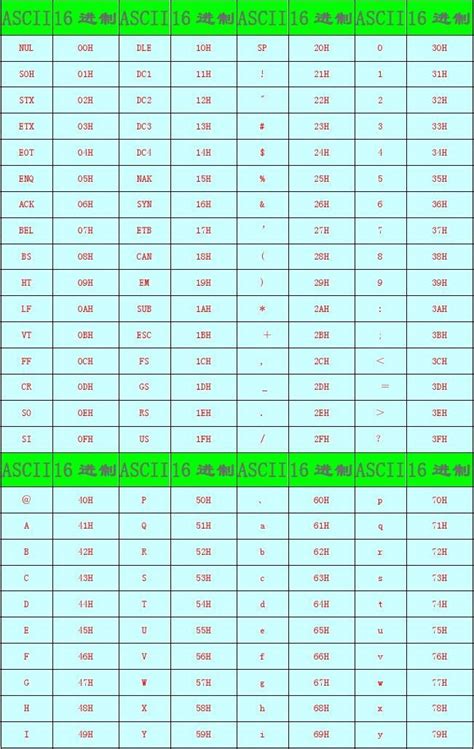
十六进制(Hex),顾名思义,是基于16的一种数制系统。它使用0到9这十个数字以及A到F这六个字母(分别代表10到15)来表示数值。这种数制的优势在于能够用较短的字符序列表示较大的数值,非常适合于计算机内存地址的表示以及颜色编码等场景。

将十六进制数转换为十进制数的过程相对简单,只需将每一位上的数值乘以16的相应次方(从右至左,最右边的位为16^0,向左依次递增),然后将所有结果相加即可。

例如,十六进制数1A3转换为十进制数的步骤如下:

1 * 16^2 = 256
A(即10) * 16^1 = 160
3 * 16^0 = 3
将上述三个结果相加:256 + 160 + 3 = 419,因此,十六进制数1A3等于十进制数419。
将十进制数转换为十六进制数,则需要采用“除16取余法”。具体步骤为:
1. 将十进制数除以16,记录余数。
2. 将商继续除以16,再次记录余数,直到商为0为止。
3. 将所有余数从最后一个开始,依次排列,若余数小于10,则直接写出数字;若余数大于等于10,则使用A-F代替(10对应A,11对应B,以此类推)。
例如,将十进制数255转换为十六进制数:
255 ÷ 16 = 15(商)余15(F)
15 ÷ 16 = 0(商)余15(F)
因此,十进制数255对应的十六进制数为FF。
由于十六进制数的每一位都可以直接映射为4位的二进制数(因为2^4=16),因此十六进制转二进制的过程相当直接:将十六进制数的每一位分别转换为对应的4位二进制数,然后拼接起来即可。
例如,十六进制数1A3转换为二进制数的步骤如下:
1 -> 0001
A(即10)-> 1010
3 -> 0011
拼接后得到:0001 1010 0011,即十六进制数1A3等于二进制数110100011。
将二进制数转换为十六进制数,则需将二进制数从右至左每4位为一组(若不足4位,则在左边补0),然后每组转换为对应的十六进制数。
例如,二进制数110100011转换为十六进制数的步骤如下:
1101(第1-4位)-> D
0001(第5-8位)-> 1
(由于第9-12位不存在,故补0凑足4位,即0000,不参与转换)
因此,二进制数110100011对应的十六进制数为1D3(注意,这里的0001直接转换为1,省略了前导的0)。
在计算机科学中,内存地址通常以十六进制形式表示,这是因为十六进制能够简洁地表示较大的数值范围,同时与计算机内部的数据存储方式(基于二进制)高度契合。例如,在32位系统中,一个内存地址可以表示为8位的十六进制数(因为2^32 = 4,294,967,296,远大于16^8 = 4294967296的表示范围,但考虑到实际使用中地址不会全部用到,故8位十六进制足以表示大多数情况下的内存地址)。
在网页设计和图像处理中,颜色通常以十六进制形式表示。一个颜色值由红、绿、蓝三个分量组成,每个分量占用8位(即一个字节),总共24位,可以表示为6位的十六进制数(两位表示一个分量)。例如,FFFFFF表示白色,其中FF分别代表红、绿、蓝三个分量达到最大值,即纯白色。
在数据通信和存储领域,十六进制也常被用来表示和传输数据。这是因为十六进制能够清晰地划分字节边界(每两位十六进制数代表一个字节),便于数据的解析和处理。例如,在网络通信协议中,数据包的头部信息、校验码等常采用十六进制格式表示。
十六进制作为一种高效的数制表示方法,在计算机科学、电子工程以及信息技术等多个领域发挥着重要作用。掌握十六进制与十进制、二进制之间的转换方法,不仅有助于深入理解计算机内部的工作原理,还能在实际应用中提高数据处理和编码的效率。通过本文的介绍,读者应该能够熟悉十六进制的基本概念、转换方法以及实际应用场景,为进一步学习和实践打下坚实的基础。
11.63M坚果时钟
78.12M一年级上册语文助手
14.89M大象库app官方
65.01Mboodo波动星球
90.92M快快查汉语字典最新版
92.37M天堂之刃
92.78M新斗罗大陆单机版
55.62M虫虫助手苹果版安装包下载
47.95M小小帝国游戏
21.45M吉林家医手机app v1.4.3
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2