二进制与十六进制转换指南：轻松掌握转换技巧

二进制和十六进制是计算机科学中非常重要的数制系统。在计算机内部，所有的数据都是以二进制的形式存储和处理的，而十六进制则因其简洁的表示方式，常用于显示和记录二进制数据。本文将详细介绍二进制和十六进制之间的转换方法，帮助读者全面理解并掌握这一技能。

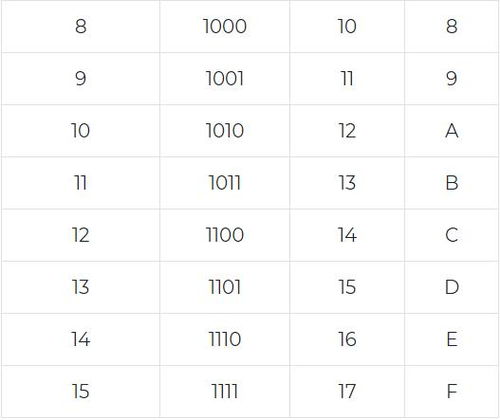
首先，我们需要了解二进制和十六进制的基本概念。二进制数制只有0和1两个数字，每一位（bit）只能是0或1。它是计算机内部处理信息的基础。而十六进制数制有0到9以及A到F共16个数字，其中A到F分别代表10到15。十六进制通常用于表示较大范围的二进制数，因为它可以用更少的位数表示相同的数值范围。

一、二进制转十六进制

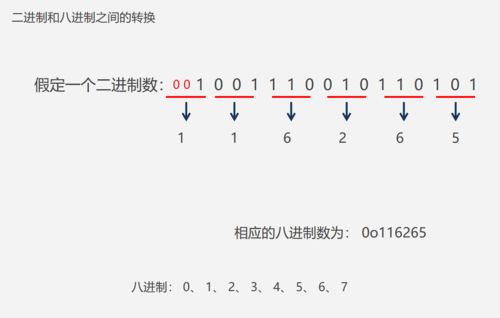
将二进制数转换为十六进制数，我们可以遵循以下步骤：

1. 分组：将二进制数从右向左每四位一组进行划分。如果最左边不足四位，则向前补0，直到所有二进制位都被包含在内。例如，二进制数1101011可以划分为0011 0101 1。

2. 转换：将每一组的四位二进制数转换为对应的十六进制数。根据二进制到十六进制的对应关系表，我们可以知道：

0000对应0

0001对应1

0010对应2

0011对应3

0100对应4

0101对应5

0110对应6

0111对应7

1000对应8

1001对应9

1010对应A

1011对应B

1100对应C

1101对应D

1110对应E

1111对应F

因此，0011对应3，0101对应5，1（不足四位，但代表0001）对应1。

3. 合并：将转换后的十六进制数字按原来的顺序合并起来，得到最终的十六进制数。所以，二进制数1101011转换为十六进制数为351。

二、十六进制转二进制

将十六进制数转换为二进制数，我们可以遵循以下步骤：

1. 拆分：将十六进制数的每一位数字单独拆分出来。例如，十六进制数3A7可以拆分为3、A、7。

2. 转换：将每一位十六进制数字转换为对应的四位二进制数。根据十六进制到二进制的对应关系表，我们可以知道：

0对应0000

1对应0001

2对应0010

3对应0011

4对应0100

5对应0101

6对应0110

7对应0111

8对应1000

9对应1001

A对应1010

B对应1011

C对应1100

D对应1101

E对应1110

F对应1111

因此，3对应0011，A对应1010，7对应0111。

3. 合并：将转换后的二进制数字按原来的顺序合并起来，得到最终的二进制数。所以，十六进制数3A7转换为二进制数为0011 1010 0111。通常，我们可以省略掉二进制数前面的0（只要它们不是有效数字的一部分），因此最终的二进制数为1110100111。

三、实际应用中的注意事项

在实际应用中，进行二进制和十六进制转换时，我们需要注意以下几点：

1. 字节单位：在计算机科学中，一个字节（Byte）通常由8位（bit）组成。因此，在转换时，我们经常需要处理的是以字节为单位的二进制和十六进制数。

2. 大小端序：在存储和传输数据时，有时会遇到大端序（Big Endian）和小端序（Little Endian）的问题。大端序是指高位字节存放在内存的低地址端，而小端序是指低位字节存放在内存的低地址端。在进行二进制和十六进制转换时，需要明确数据的存储方式，以确保转换的正确性。

3. 校验和：在某些应用场景中，为了检测数据的完整性，我们可能会使用校验和（Checksum）技术。在进行二进制和十六进制转换时，需要确保校验和的正确计算，以避免数据在传输或存储过程中发生错误。

4. 编程实现：在实际编程中，许多编程语言都提供了内置的函数或方法来进行二进制和十六进制的转换。例如，在Python中，我们可以使用`bin()`函数将十进制数转换为二进制数，使用`hex()`函数将十进制数转换为十六进制数；在C语言中，我们可以使用`printf`函数的格式化输出选项来进行转换。了解和掌握这些编程技巧可以大大提高我们的工作效率。

综上所述，二进制和十六进制之间的转换是计算机科学中的一项基本技能。通过本文的介绍，相信读者已经对二进制和十六进制的转换方法有了全面的了解。在实际应用中，我们需要根据具体的需求和场景来选择合适的转换方法，并注意相关的注意事项，以确保数据的正确性和完整性。