在数学的世界里,三位数除一位数是一种常见的运算类型,它不仅在学生的基础教育中占据重要位置,也是日常生活中频繁遇到的计算场景。这种运算不仅锻炼了我们的逻辑思维能力,还提高了我们处理数字的效率。本文将从定义与基本规则、实例解析、实际应用、学习技巧以及在教育中的应用与影响等多个维度,深入探讨三位数除一位数的内涵与外延。
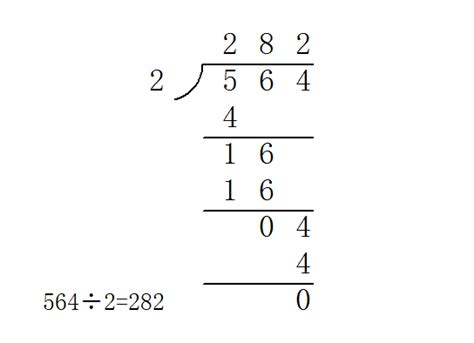
三位数除一位数,简而言之,就是用一个一位数去除一个三位数,得出商和(可能存在的)余数的过程。例如,用7去除490,即490÷7,其结果是70,余数为0。这一过程遵循除法的基本规则:被除数=除数×商+余数。这个规则是进行除法运算的基础,也是检查运算结果正确性的重要依据。

为了更好地理解三位数除一位数,让我们通过几个实例来进行分析。

1. 456÷3

分析:这是一个典型的三位数除以一位数的例子。首先,我们看被除数百位上的4,它小于除数3,因此无法直接除,我们需要将45一起考虑。45÷3=15,没有余数,因此我们在商的百位上写1,十位上暂留空位。接下来,将被除数十位上的6落下来,得到6(实际上是06,但前导0可省略),6÷3=2,将2写在商的十位上。所以,456÷3=152。

结果:152
2. 789÷9
分析:在这个例子中,被除数百位上的7大于除数9,但78大于9且小于81(9的9倍),所以我们可以直接处理到十位。78÷9=8余6,我们在商的百位上写0(因为不够除),十位上写8,然后将被除数个位上的9落下来,得到69。69÷9=7余6,将7写在商的个位上,余数保留。
结果:87余6,或表示为87.67(以小数形式表示余数,即6/9≈0.67,但通常我们会保留整数商和明确的余数)
3. 999÷9
分析:这是一个特殊情况,因为被除数每一位上的数字都是9的倍数。99÷9=11,没有余数,将9(被除数个位)落下来后,9÷9=1,也没有余数。
结果:111
三位数除一位数在日常生活中有着广泛的应用,从简单的购物计算到复杂的财务管理,都离不开这一基本运算。
购物打折:在购物时,如果商品原价是三位数,而你想知道在某个折扣率下需要支付多少钱,就需要用到除法。例如,一件原价999元的商品打7折,就需要计算999÷7(实际上是999×0.7,但这里为了强调除法应用,我们转换成除法形式),结果是约700元。
预算管理:在个人或企业的预算管理中,经常需要分配资源或计算成本。比如,如果某公司年度预算为300,000元,需要分配到10个部门,每个部门获得的预算就是300,000÷10=30,000元。
时间分配:在学习或工作中,合理规划时间至关重要。比如,如果你有240分钟(4小时)的学习时间,需要分配到4门科目上,每门科目的学习时间就是240÷4=60分钟。
对于初学者来说,掌握三位数除一位数可能有一定的难度。以下是一些有效的学习技巧:
理解除法概念:首先要明确除法的含义,即“分组”或“平均分配”。这有助于理解为什么除法运算会产生商和余数。
分步练习:从简单的两位数除一位数开始,逐步过渡到三位数除一位数。分步练习可以帮助建立信心,逐步掌握技巧。
利用工具:利用计算器或数学软件进行验证,确保自己的计算准确无误。同时,也可以利用这些工具探索不同的数学模式,如被除数、除数、商和余数之间的关系。
实际操作:通过日常生活中的实际问题进行练习,如购物、烹饪时的分量分配等,将数学知识应用于实践,可以加深理解。
在数学教育中,三位数除一位数是培养学生逻辑思维和问题解决能力的重要环节。它不仅要求学生掌握基本的算术运算技巧,还要求学生能够理解并应用这些技巧解决实际问题。
培养逻辑思维:除法运算需要按照一定的逻辑顺序进行,从高位到低位,逐步求解。这有助于培养学生的逻辑思维能力和条理性
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2