揭秘！长方体体积计算公式全解析

在探讨几何学的广阔领域中，长方体作为一种基础且重要的三维形状，其体积的计算是理解和应用空间概念的关键一环。长方体，顾名思义，是一个拥有六个矩形面的多面体，每个面都与另一个面平行且等长等宽（对于相对的面而言）。它的特性使得体积计算既直观又富有教育意义，适合作为引入三维空间几何概念的良好起点。

长方体的基本构造

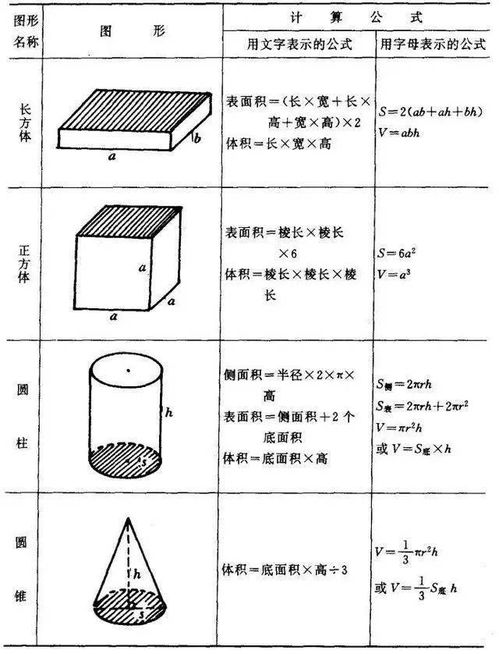
首先，让我们简要回顾长方体的基本构造。一个长方体由三组平行的、等长的棱组成，这三组棱分别代表长方体的长（L）、宽（W）和高（H）。长方体的每一个顶点都由这三组棱相交而成，而它的六个面则分别由这些棱围合形成，每两个相对的面都是全等的矩形。

长方体体积的概念

体积，在几何学中，是描述一个物体占据空间大小的量度。对于长方体而言，其体积即为它所占据的三维空间大小。理解这一点，是掌握长方体体积计算公式的前提。

长方体体积的计算公式

长方体的体积计算公式简单而直观，它直接关联到长方体的三个维度：长（L）、宽（W）和高（H）。具体来说，长方体的体积V可以通过以下公式计算得出：

\[ V = \text{长} \times \text{宽} \times \text{高} \]

即：

\[ V = L \times W \times H \]

这个公式不仅揭示了长方体体积与其三个维度之间的直接联系，还体现了三维空间中“体积是面积在高度方向上的累积”这一基本思想。

公式推导与应用

虽然长方体的体积公式看似简单，但其背后蕴含着丰富的几何直觉和逻辑推理。从二维到三维的跨越，不仅仅是增加了一个维度那么简单，它要求我们对空间有更加深入的理解。

推导过程：可以想象将长方体沿其长度方向“切片”，每一片都是一个与底面相同大小的矩形，其面积即为长乘以宽（L×W）。然后，将所有这些“切片”沿着高度方向堆叠起来，所有切片的总面积之和（即所有矩形的面积之和）再乘以它们的高度H，就得到了长方体的体积。这个过程实质上就是面积在高度方向上的积分，尽管在初等几何中我们并不使用这样的术语。

应用实例：长方体的体积公式在日常生活和工程领域中有着广泛的应用。比如，在建筑设计中，需要计算所需材料的体积以估算成本；在物流管理中，了解货物的体积对于优化装载和运输至关重要；在科学实验中，精确测量溶液的体积是确保实验准确性的基础。

深入理解长方体的体积

除了掌握公式本身外，深入理解长方体体积的概念还能帮助我们更好地应用它。以下几点值得注意：

1. 单位的一致性：在计算长方体的体积时，必须确保长度、宽度和高度的单位相同，否则结果将失去意义。常见的体积单位有立方厘米（cm³）、立方分米（dm³）、立方米（m³）等。

2. 体积的相对性：长方体的体积是相对于其所在空间而言的。改变长方体的尺寸（长、宽、高中的任何一个或多个），其体积都会相应变化。

3. 与表面积的区别：长方体的体积描述的是它占据的空间大小，而表面积则是其外表面所覆盖的面积之和。两者虽然都与长方体的尺寸有关，但衡量的是不同的物理量。

4. 三维空间的直观感受：通过亲手制作长方体模型、观察身边的长方体物体等方式，可以增强对三维空间及长方体体积的直观感受和理解。

结语

长方体的体积公式是几何学中一个基础而重要的知识点，它不仅教会我们如何计算一个具体形状的三维空间大小，还引导我们深入探索三维空间的奥秘。通过理解和应用这一公式，我们能够更好地理解和解决与三维空间相关的问题，为进一步学习更高级的几何知识和物理概念打下坚实的基础。同时，这也提醒我们，在探索未知世界的过程中，保持好奇心和求知欲是至关重要的。