正方体的表面积计算公式是什么？

在几何学的广阔天地中，正方体作为一种基础而重要的三维形状，其独特的属性与计算方式始终吸引着无数学者的目光。正方体，顾名思义，是一个所有棱长都相等的特殊长方体，其六个面均为正方形，这一特性使得它在面积和体积的计算上呈现出独特的规律。今天，我们就从多个维度出发，深入探讨正方体的面积公式及其背后的几何逻辑与实际应用。

一、正方体的基本构造

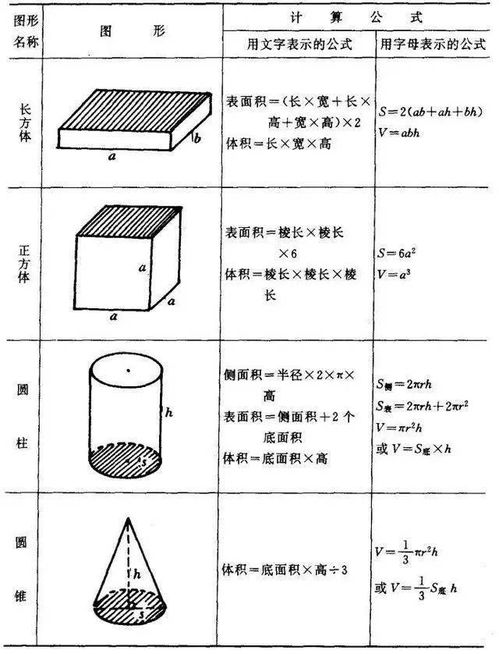
首先，让我们从正方体的基本构造说起。正方体由六个面、十二条棱和八个顶点组成。每个面都是一个正方形，所有棱的长度都相等，这一等长的特性是正方体区别于其他长方体的关键。正方体的这种均匀性不仅赋予了它视觉上的美感，也为后续的面积和体积计算提供了便利。

二、正方体的面积计算：理论探索

1. 单个面的面积

要计算正方体的总面积，首先需要知道单个正方形面的面积。正方形面积的计算公式是边长的平方，即 $S = a^2$，其中 $a$ 是正方形的边长，也即正方体的棱长。这是面积计算的基础，也是理解正方体总面积公式的起点。

2. 正方体的总面积

正方体有六个完全相同的面，因此，其总面积就是这六个面面积的总和。将单个面的面积 $a^2$ 乘以6，即得正方体的总面积公式：$S_{\text{total}} = 6a^2$。这个公式简洁而直观，体现了正方体面积计算的精髓。

三、多维度的理解与应用

1. 几何视角：空间与形状

从几何学的角度来看，正方体面积的计算不仅仅是一个数学公式的应用，更是对空间与形状关系的深刻理解。正方体作为三维空间中的一种基本形状，其面积的计算帮助我们认识到，在三维世界中，物体占据的空间不仅可以通过体积来衡量，其表面的覆盖面积也是一个重要的属性。这种认识对于建筑设计、包装工程、材料科学等领域都具有重要的指导意义。

2. 数学逻辑：代数与几何的结合

正方体的面积公式 $S_{\text{total}} = 6a^2$ 是代数与几何完美结合的典范。它通过将几何形状（正方体）的属性（边长 $a$）代入到代数表达式中，得到了一个简洁的数值结果（总面积）。这种结合不仅简化了计算过程，也展示了数学在解决实际问题时的强大力量。

3. 物理应用：表面积与热传导

在物理学领域，正方体的面积计算同样具有重要意义。例如，在热传导问题中，物体的表面积是决定其散热速度的关键因素之一。正方体作为一个简单的几何模型，其表面积的计算为研究物体在特定环境下的热交换过程提供了基础数据。此外，在材料科学中，涂料的用量、电镀的表面积等都与物体的表面积密切相关，正方体面积的计算公式在此类问题中发挥着不可或缺的作用。

4. 教育意义：培养空间想象力

对于学生而言，正方体面积的计算不仅仅是一个知识点的掌握，更是培养空间想象力和几何直觉的重要途径。通过学习正方体面积的计算过程，学生可以更加直观地理解三维空间中的形状与尺寸关系，为后续学习更复杂的几何知识和解决实际问题打下坚实的基础。

四、结语

综上所述，正方体的面积公式 $S_{\text{total}} = 6a^2$ 不仅是数学中的一个基本公式，更是连接几何、代数、物理等多个学科的桥梁。通过对正方体面积的计算与探索，我们不仅可以加深对空间与形状的理解，还能感受到数学在解决实际问题中的广泛应用和无穷魅力。因此，无论是从理论学习的角度还是实践应用的角度来看，掌握正方体面积的计算方法都是极其重要的。在未来的学习和生活中，让我们继续探索几何的奥秘，感受数学的美丽与力量。