请问正方体的表面积计算公式是怎样的？

在探索几何学的广袤领域中，正方体作为三维空间中最基础且最具代表性的多面体之一，其性质与计算方法一直是学习数学时不可或缺的部分。正方体，顾名思义，是一个拥有六个面且每个面均为正方形的立体图形。这一特性使得它在计算面积时既展现出一定的规律性，也蕴含着丰富的几何原理。那么，当我们聚焦于“正方体的面积公式是什么”这一问题时，实际上是在询问如何计算正方体所有外表面（不包括内部）的总面积。

正方体的基本构造

首先，让我们简要回顾正方体的基本构造。正方体由六个完全相同的正方形面组成，这些面两两平行且垂直相交于棱线。每条棱线都是两个相邻正方形面的公共边，且所有棱线的长度都相等，我们称之为正方体的棱长。这一均匀对称的结构为计算其面积提供了便捷。

正方体的面积计算

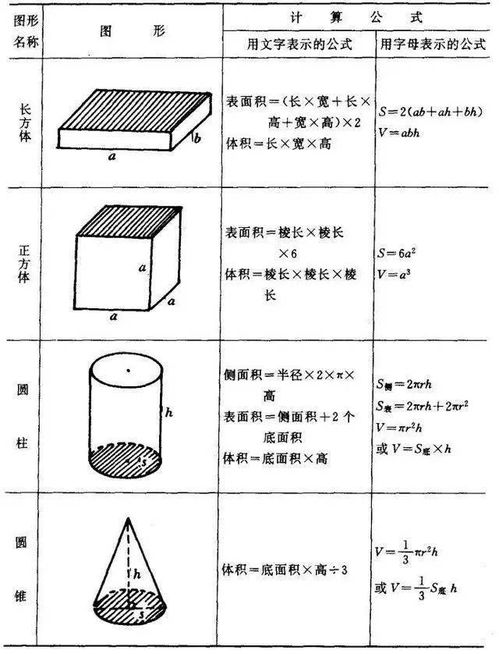
正方体的面积，通常指的是其所有外表面（即六个正方形面）的面积之和。由于每个面都是正方形，其面积计算公式为“边长的平方”（即 $a^2$，其中 $a$ 为正方形的边长）。对于正方体而言，所有面的边长都是相同的，即正方体的棱长。

因此，要计算正方体的总表面积，我们只需将一个正方形面的面积乘以6（因为正方体有六个这样的面）。用数学表达式表示即为：

$$ \text{正方体表面积} = 6 \times a^2 $$

其中，$a$ 是正方体的棱长。

应用实例

为了更好地理解这一公式，我们可以通过一个简单的实例来演示其应用。假设我们有一个棱长为5厘米的正方体，想要计算它的总表面积。

1. 确定棱长：首先，明确正方体的棱长为5厘米，即 $a = 5 \text{ cm}$。

2. 计算单个正方形面的面积：根据正方形面积的计算公式 $a^2$，我们得到一个正方形面的面积为 $5^2 = 25 \text{ 平方厘米}$。

3. 计算总表面积：然后，将这个面积乘以6（因为正方体有六个面），得到总表面积为 $6 \times 25 = 150 \text{ 平方厘米}$。

正方体面积公式的意义

正方体面积公式的意义远不止于简单的数值计算。它不仅是解决实际问题（如包装材料的需求、建筑物外墙涂料的估算等）的重要工具，还深刻体现了几何学中的对称性与比例关系。通过这个公式，我们可以直观地感受到三维空间与二维平面之间的紧密联系，以及如何通过二维量的累加来描述三维对象的特性。

拓展思考

进一步地，正方体面积的计算还可以引申出对更复杂几何体表面积的探索。例如，长方体作为正方体的一个广义形式，其表面积的计算虽然也基于相似的原理，但需要考虑不同边长对面积的影响。此外，通过正方体的表面积计算，我们还可以进一步理解到体积与表面积之间的关系，这在物理学、工程学等多个领域都具有重要应用。

总之，“正方体的面积公式是什么”这一问题，不仅是一个简单的数学知识点，更是通向更广阔数学世界和实际应用领域的一把钥匙。通过深入理解和应用这一公式，我们能够更加灵活地解决各类与几何表面积相关的问题，同时也能够更深刻地感受到数学与现实生活之间的紧密联系。