在数据分析的广阔世界里,频率分布直方图是一种强有力的工具,它能够帮助我们直观地了解数据的分布情况。而在这些分布图中,中位数作为一个重要的统计量,扮演着衡量数据中心位置的关键角色。今天,我们就来深入浅出地探讨一下“频率分布直方图中位数的公式是什么”,以及它是如何在实际应用中发挥作用的。
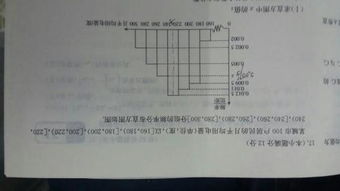
首先,让我们从基础开始。频率分布直方图是一种特殊的统计图表,它通过一系列矩形条(或称为柱子)来表示数据的分布情况。在这个图表中,横轴代表数据的不同取值范围(即组距),而纵轴则表示每个取值范围内数据的频率(或称为频数除以组距)。这种图表的好处在于,它能够清晰地展示数据在各个区间的分布情况,让我们一眼就能看出数据的集中趋势和离散程度。

在深入讲解中位数公式之前,我们先来明确一下中位数的定义。中位数是指一组数据按照大小顺序排列后,位于中间位置的那个数。如果数据量是奇数,则中位数就是正中间的数;如果数据量是偶数,则中位数通常是中间两个数的平均值。在频率分布直方图中,中位数同样代表着数据的中心位置,但由于数据是以区间的形式展示的,所以我们需要通过特定的方法来计算它。

在频率分布直方图中,计算中位数的关键在于找到那个使得左右两侧数据面积(或称为频率)相等的点。由于直方图是用矩形的面积来表示频率的,因此中位数就是使得左右两侧矩形面积和为0.5(即总面积的一半)的那个点所对应的横坐标值。
具体来说,我们可以按照以下步骤来计算中位数:
1. 确定中位数所在的区间:
首先,我们需要找到那个包含中位数的区间。这通常是通过累加各区间的频率(或面积)来实现的,直到累加值首次超过或等于0.5为止。这个区间就是中位数所在的区间。
2. 应用公式计算中位数:
一旦确定了中位数所在的区间,我们就可以使用公式来计算中位数的具体值了。这个公式通常可以表示为:
\[
\text{中位数} = \text{区间左边界} + \frac{(\text{区间右边界} - \text{区间左边界}) \times (\text{总频率} - \text{之前区间频率总和})}{2 \times \text{当前区间频率} - (\text{总频率} - 0.5)}
\]
但是,请注意,上述公式可能因不同的教材或资料而有所差异。在实际应用中,更常用的方法是利用直方图的几何性质,即找到使得左右两侧矩形面积和为0.5的那个点的横坐标值。这通常可以通过目测或使用简单的算术计算来实现。
一个更直观的方法是:假设我们已经找到了中位数所在的区间[a, b),并且这个区间以及之前所有区间的总频率为p(p小于或等于0.5),当前区间的频率为q。那么,中位数就可以通过以下方式估算出来:
\[
\text{中位数} \approx a + \frac{(b - a) \times (0.5 - p)}{q}
\]
这个公式实际上是在说:从区间的左边界a开始,加上一个调整量,这个调整量是根据中位数应该落在的位置(即0.5的位置)和当前已经累加的频率p来计算的。具体来说,就是用区间宽度(b-a)乘以剩余需要达到的频率(0.5-p),再除以当前区间的频率q,从而得到需要向右移动的距离。
在使用频率分布直方图计算中位数时,我们需要注意以下几点:
确保数据的完整性:在计算之前,需要确保所有的数据都已经正确地被收集并整理到了直方图中。
合理选择组距:组距的选择对直方图的形状和中位数的计算都有重要影响。如果组距过大,可能会掩盖数据的细节;如果组距过小,则会使直方图过于复杂而难以解读。
注意边界效应:在计算过程中,要注意边界效应对结果的影响。特别是在确定中位数所在的区间时,要特别小心不要将中位数误判到相邻的区间中。
结合实际情况进行解读:最后,我们还需要结合实际情况对计算结果进行解读。比如,在某些情况下,中位数可能并不能完全代表数据的中心位置,这时我们就需要结合其他统计量(如平均数、众数等)来进行综合分析。
通过上述的介绍,相信大家对“频率分布直方图中位数的公式是什么”这个问题已经有了更加清晰的认识。中位数作为衡量数据中心位置的重要指标,在数据分析中扮演着举足轻重的角色。而频率分布直方图则为我们提供了一种直观、便捷
63.93M阳光趣爱
48.53M号令天下手机版
97.06Martand艺术社交平台
17.46M大管家巡航系统
20.27M速漫库app安卓版
0B西西漫画去广告版
93.25M速看短剧2026
39.98M快对作业2026最新版
40.36M饭团探书旧版本大全
18.50M这就是警察手游安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2