数学统计图：深入解析众数、平均数、中位数的计算方法与应用

在数学领域中，统计图作为数据可视化的一种重要工具，能够直观地展现数据的分布特征和变化趋势。而众数、平均数（算术平均数）、中位数作为描述数据集特征的三个核心概念，对于理解数据的集中趋势尤为关键。本文将深入浅出地介绍如何在统计图中识别和应用这三个统计量，帮助读者更全面地把握数据背后的信息。

引言

在日常生活中，我们时常需要处理和分析各种数据，比如考试成绩、销售数据、人口统计等。为了更有效地传达数据的内在信息，人们发明了多种统计图，如条形图、折线图、直方图、箱线图等。同时，为了量化数据的集中趋势，引入了众数、平均数和中位数等统计量。了解这些统计量的计算方法和在统计图中的表现，对于数据分析、决策制定等具有重要意义。

众数（Mode）

定义

众数是指在一组数据中出现次数最多的数值。当数据中存在多个众数时（即多个数值的出现次数相同且最多），这组数据被称为多众数数据。

在统计图中的识别

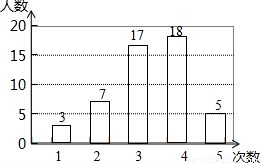
条形图：在条形图中，众数通常表现为最长（或最高）的条。如果多个条的高度相同且最高，则这些条对应的数值都是众数。

直方图：直方图用于表示连续型数据的分布情况。众数所在区间将是直方图中最高的柱子（或柱子之一），即该区间内的数据点最为集中。

其他图表：虽然众数在箱线图等某些统计图中不直接显示，但通过观察数据的整体分布，可以间接推断出可能的众数范围。

应用

众数在描述非数值型数据（如最受欢迎的颜色、最流行的电影类型）或具有明显集中点的数值型数据中非常有用。然而，需要注意的是，众数可能不存在（如数据分布均匀时），或存在多个（如双峰分布）。

平均数（Arithmetic Mean）

定义

平均数是所有数据的和除以数据的个数得到的。它反映了数据集的“平均水平”或“中心位置”。

在统计图中的计算与理解

计算：平均数不直接通过统计图得出，而是需要先将图中的数据提取出来，进行求和与平均。

理解：在条形图、折线图中，平均数通常不是一个直接可见的点，但可以通过连接各数据点的趋势线来大致估计。在直方图中，平均数的位置可以通过考虑数据的整体分布来推测，它可能位于数据分布的中心附近，但并不一定是分布的高峰点。

应用

平均数因其计算简便、易于理解而被广泛应用。然而，它也受到极端值的影响较大，因此在数据差异显著或存在异常值时，平均数可能无法准确反映数据的真实集中趋势。

中位数（Median）

定义

中位数是将一组数据从小到大排列后，位于中间位置的数。如果数据量是奇数，则中位数是正中间的数；如果数据量是偶数，则中位数是中间两个数的平均值。

在统计图中的识别

排序数据图：在将数据排序后绘制的条形图或折线图中，中位数直接对应于中间的条（或点）。对于偶数数据量，中位数为中间两个点的中间值，需通过计算得出。

箱线图：箱线图是展示数据分布特征的一种直观方式，其中位数直接由箱子中间的线表示，这条线称为中位数线，它准确地标出了数据的中位数。

直方图：虽然直方图本身不直接显示中位数，但通过观察数据的累积频率分布，可以估计出中位数的位置。

应用

中位数不受极端值的影响，因此在数据分布偏斜或存在异常值时，中位数更能代表数据的中心位置。此外，中位数在计算上也相对简单，易于理解和应用。

结语

众数、平均数和中位数作为描述数据集特征的三大统计量，各自具有独特的应用场景和优缺点。在理解和运用这些统计量时，我们需要结合具体的统计图和数据特点，灵活选择并恰当解释。通过掌握这些基础统计概念，我们能够更深入地洞察数据背后的规律和趋势，为决策制定提供有力的支持。同时，也应注意到统计量的局限性，避免在复杂的数据环境中盲目依赖单一统计量而导致误判。