在探讨数学领域中,函数值域的求解问题一直是学习与分析的重点。值域,作为函数的一个重要属性,描述了函数输出值的所有可能集合。掌握多种求解方法,不仅能深化对函数本质的理解,还能在面对复杂问题时迅速找到解决方案。以下将详细介绍几种常用的函数值域求解方法,包括观察法、代数法、图像法、单调性法以及换元法,旨在帮助读者全面提升解决此类问题的能力。
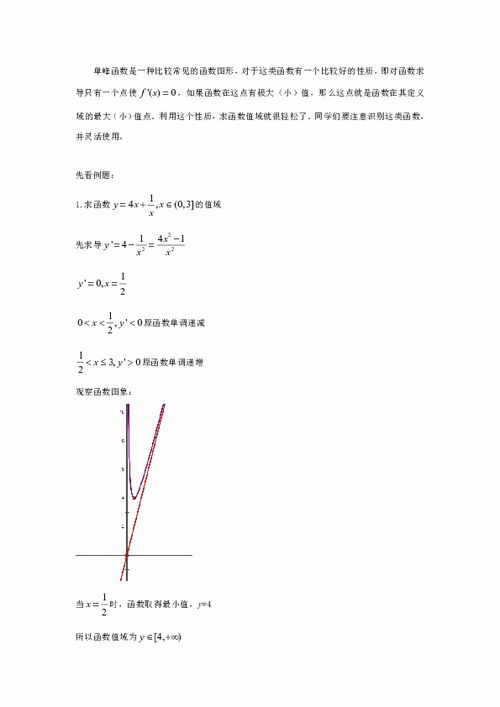
观察法是最直观且适用于简单函数的一种求解方法。通过观察函数的表达式,直接根据函数的定义域、系数及运算性质,推断出函数值的可能范围。例如,对于线性函数y=ax+b(a≠0),其值域为全体实数集R,因为无论x取何值,y都能取到所有实数。再如,对于常数函数y=c,其值域显然为单元素集合{c}。对于形如y=x^2(x∈R)的二次函数,由于平方运算的结果总是非负的,因此其值域为[0,+∞)。观察法的关键在于对函数形式的熟悉与敏感,能够快速识别函数特性,从而直接得出值域。

代数法适用于能够通过代数变换求解值域的函数。这种方法的核心在于将原函数进行等价变形,转化为更易分析的形式。常见的代数变换包括配方、因式分解、完成平方等。以二次函数y=ax^2+bx+c(a≠0)为例,通过配方将其转化为顶点式y=a(x-h)^2+k,可以直观地看出函数的最小值或最大值(取决于a的正负),从而确定值域。对于分式函数,如y=(px+q)/(rx+s),可以通过有理化处理,消去分母,转化为整式函数求解值域。代数法的优势在于能够处理较为复杂的函数形式,但需要较高的代数运算技巧。

图像法是借助函数图像直观展示函数值域的方法。通过绘制函数图像,观察图像在坐标平面上的分布特征,如最高点、最低点、渐近线等,可以直观判断函数的值域。例如,对于正弦函数y=sinx,其图像呈现周期性波动,最大值为1,最小值为-1,因此值域为[-1,1]。对于指数函数y=a^x(a>0且a≠1),其图像随着x的增大或减小而无限上升或下降,因此值域为(0,+∞)(当a>1)或(-∞,0)(当0
63.93M阳光趣爱
48.53M号令天下手机版
97.06Martand艺术社交平台
17.46M大管家巡航系统
20.27M速漫库app安卓版
0B西西漫画去广告版
93.25M速看短剧2026
39.98M快对作业2026最新版
40.36M饭团探书旧版本大全
18.50M这就是警察手游安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2