探索多种求解斜率k的神奇公式！

在数学领域中，求斜率k的公式是解析几何与函数图像分析的基础。无论是直线方程、曲线切线，还是函数图像的导数表示，斜率都扮演着至关重要的角色。以下是一篇关于求斜率k公式的详尽探讨，旨在通过不同的角度和场景，展现斜率求解的多样性和灵活性。

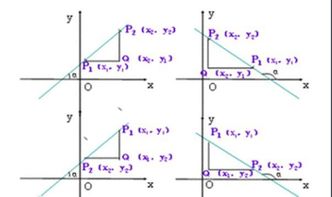
在平面直角坐标系中，一条直线的斜率k描述了其倾斜程度。最基础的斜率公式来自于直线的两点式。给定直线上的两点(x1, y1)和(x2, y2)，斜率k可以通过以下公式求得：k = (y2 - y1) / (x2 - x1)。这个公式直观反映了直线上两点间垂直距离与水平距离的比值，即直线的倾斜程度。

除了两点式，直线方程也是求解斜率的重要途径。直线的点斜式方程为y - y1 = k(x - x1)，其中(x1, y1)是直线上的一点，k是直线的斜率。如果已知直线上的一点和直线的倾斜角α，斜率k还可以通过斜率与倾斜角的关系式k = tanα求得。这里的tan表示正切函数，倾斜角α是直线与x轴正方向之间的夹角，且α的取值范围为[0, π)，即0度到180度（不包含180度）。

当直线方程以一般式Ax + By + C = 0给出时，斜率k的求解需要稍作变换。此时，斜率k可以通过-A/B求得，前提是B不等于0。这个公式来源于将一般式方程转化为斜截式y = -Ax/B - C/B的过程，其中-Ax/B表示了x的系数与y的系数之比，即直线的斜率。

在解析几何中，直线与圆、椭圆、抛物线等曲线的切点处，切线的斜率也是重要的研究对象。对于一般的二次曲线f(x, y) = 0，其在点(x0, y0)处的切线斜率k可以通过对该曲线方程在(x0, y0)点处求偏导数，并利用偏导数的关系求得。例如，对于抛物线y = ax^2 + bx + c，其在点(x0, y0)处的切线斜率k为2ax0 + b。

在函数图像的分析中，斜率k与函数的导数紧密相关。对于可导函数y = f(x)，其在点x0处的导数f'(x0)即为该点处切线的斜率。导数的几何意义在于，它描述了函数图像在某点处的倾斜程度，即该点处切线的斜率。通过求导，我们可以得到函数在整个定义域内各点处的切线斜率，进而分析函数的单调性、极值点等性质。

此外，斜率k在直线与坐标轴的夹角计算中也有着重要应用。已知直线的斜率k，我们可以求出直线与x轴的夹角α的正切值tanα = k，进而通过反正切函数arctan(k)求得夹角α的具体度数。这个夹角反映了直线在平面直角坐标系中的方向性。

在直线的垂直与平行关系中，斜率也发挥着关键作用。如果两条直线的斜率分别为k1和k2，那么当k1 = k2时，这两条直线平行；当k1 = -1/k2时，这两条直线垂直。这一性质在判断直线的相对位置关系中具有重要意义。

在三维空间中，直线的斜率概念被直线的方向向量所替代。但即便如此，斜率的思想仍然在其中有所体现。例如，在三维空间中给定一直线，我们可以通过其上的两点来确定一个方向向量(dx, dy, dz)，其中dx、dy、dz分别为这两点间x、y、z坐标的差。这个方向向量在某种程度上可以看作是直线在三个坐标轴方向上“斜率”的集合。

值得注意的是，在某些特殊情况下，如直线垂直于x轴时，斜率k不存在（或说为无穷大）。这是因为此时直线上的所有点的y坐标都相同，而x坐标可以任意变化，导致斜率无法定义。同样地，在曲线分析中，如果曲线在某点处不光滑或存在尖点，那么该点处的切线斜率也可能不存在。

此外，斜率k还与直线的截距式方程y = kx + b中的k相对应。这里的k表示直线的斜率，b表示直线在y轴上的截距。通过截距式方程，我们可以直观地看出斜率k对直线位置的影响：当k为正时，直线从左下方向右上方倾斜；当k为负时，直线从左上方向右下方倾斜；当k为0时，直线与x轴平行；当直线垂直于x轴时（即斜率不存在），直线方程为x = 常数形式。

综上所述，求斜率k的公式多种多样，它们分别适用于不同的场景和条件。无论是直线的两点式、点斜式、一般式方程，还是函数图像的导数表示、三维空间的方向向量等，都为我们提供了求解斜率的有效方法。掌握这些