等腰三角形面积公式是什么？已知腰长该如何求解？

等腰三角形面积公式详解及腰长求解应用

等腰三角形作为几何学中的基础图形，因其两边等长、具有对称性而备受关注。在学习等腰三角形的性质时，面积的计算是一个重要的知识点。本文将详细介绍等腰三角形的面积公式，并探讨在已知腰长的情况下如何求解面积。

一、等腰三角形的面积公式

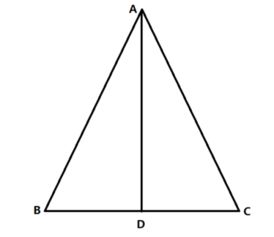
等腰三角形是两边等长的三角形，设其腰长为a，底边长为b，高为h。根据三角形面积的一般公式，面积S可以表示为底边b与高h乘积的一半，即：

S = 0.5 × b × h

在等腰三角形中，由于两边等长，可以通过勾股定理或其他几何关系求出高h。设等腰三角形的顶角为θ，则底边的一半（即b/2）与腰长a和高h之间构成直角三角形，其关系可由余弦定理或正弦定理表示。但在此，我们更关心的是如何直接求出面积，因此采用面积公式结合等腰三角形的性质进行推导。

对于等腰三角形，其高h可以通过以下方式求出：

1. 利用三角函数：若已知顶角θ，则高h = a × sin(θ/2)（因为等腰三角形的高将底边平分，形成两个相等的直角三角形，其锐角为θ/2）。

2. 利用勾股定理：若已知底边b和腰长a，则可以通过勾股定理求出高h。设底边的一半为c = b/2，则h = √(a² - c²)。

将求出的高h代入面积公式S = 0.5 × b × h，即可得到等腰三角形的面积。

二、已知腰长求面积的方法

在已知等腰三角形的腰长a的情况下，要求出面积S，还需要知道底边b或顶角θ中的至少一个参数。以下是几种常见的情况及求解方法：

1. 已知腰长a和底边b：

直接利用面积公式S = 0.5 × b × h，并结合等腰三角形的高h的求解方法（如利用勾股定理h = √(a² - (b/2)²）），求出面积S。

示例：若等腰三角形的腰长a = 5，底边b = 6，则高h = √(5² - (6/2)²) = 4，面积S = 0.5 × 6 × 4 = 12。

2. 已知腰长a和顶角θ：

利用三角函数求出高h = a × sin(θ/2)，然后代入面积公式S = 0.5 × b × h。但此时需要注意，由于只知道顶角θ和腰长a，不知道底边b，因此需要先求出b。由于等腰三角形的对称性，底边b可以通过腰长a和顶角θ的余弦值求出：b = 2 × a × cos(θ/2)。再将求出的b代入面积公式。

然而，在实际操作中，为了避免重复计算，我们可以直接利用腰长a、顶角θ和面积公式的关系进行推导。由于S = 0.5 × b × h = 0.5 × 2 × a × cos(θ/2) × a × sin(θ/2) = a² × sin(θ) × cos(θ/2)（注意这里b已被替换为2a cos(θ/2)），进一步化简可得S = 0.5 × a² × sin(θ) / cos(θ/2)（但此公式不如直接代入b和h计算直观和方便，因此更多时候还是采用先求b再求S的方法）。

示例：若等腰三角形的腰长a = 5，顶角θ = 60°，则底边b = 2 × 5 × cos(30°) = 5√3，高h = 5 × sin(30°) = 2.5（但这里直接求h并不直观，更多是为了展示三角函数的应用），面积S = 0.5 × 5√3 × 2.5 = (25√3)/4。或者更直接地，利用S = 0.5 × a² × sin(θ)（这里θ为顶角，且已知为等腰三角形，因此面积公式中的b/2 × tan(θ/2)部分可以化简为a × sin(θ/2)，再乘以2得到两边的高之和即整体的高对应的面积部分，但考虑到等腰三角形的对称性，直接乘以sin(θ)更为简洁且等价），则S = 0.5 × 5² × sin(60°) = (25√3)/4。

3. 已知腰长a和底边上的高h（注意这里的