MATLAB技巧：利用IOTransfer与du2y函数绘制Impulse响应图详解

在MATLAB中，IOTransfer函数和绘制impulse响应图是控制系统分析与设计中的重要工具。它们能够帮助工程师直观地理解系统的动态特性，从而进行有效的系统调试和优化。本文将围绕如何在MATLAB中使用IOTransfer函数并绘制impulse响应图展开，从基础概念、具体步骤、实例分析以及优化建议等多个维度进行详细阐述。

一、基础概念介绍

1.1 IOTransfer函数

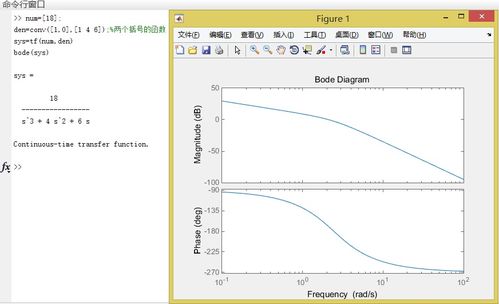
IOTransfer是MATLAB控制系统工具箱中的一个函数，用于表示线性时不变（LTI）系统的输入输出传递函数模型。传递函数是描述系统动态响应的数学工具，在频域中表示为输出与输入拉普拉斯变换的比值。IOTransfer函数可以创建单个或多个输入输出的传递函数模型，便于后续的分析和仿真。

1.2 Impulse响应图

Impulse响应图展示了系统对单位脉冲输入信号的响应。单位脉冲输入信号在t=0时刻为1，在其他时刻为0，其作用是检验系统对瞬时扰动的反应能力。Impulse响应图提供了系统时间响应的直观描述，包括系统响应的速度、稳定性和超调量等关键信息。

二、具体步骤

2.1 创建传递函数模型

首先，我们需要使用IOTransfer函数创建系统的传递函数模型。假设我们有一个简单的二阶系统，其传递函数为H(s) = ω² / (s² + 2ζωs + ω²)，其中ω是自然频率，ζ是阻尼比。

```matlab

% 定义自然频率和阻尼比

omega = 10; % 自然频率

zeta = 0.1; % 阻尼比

% 创建传递函数分子和分母多项式

numerator = [omega^2];

denominator = [1 2*zeta*omega omega^2];

% 使用IOTransfer函数创建传递函数模型

sys = tf(numerator, denominator);

```

2.2 绘制Impulse响应图

有了传递函数模型后，我们可以使用impulse函数绘制Impulse响应图。

```matlab

% 绘制Impulse响应图

figure;

impulse(sys);

title('Impulse Response of the System');

xlabel('Time (s)');

ylabel('Response');

grid on;

```

上述代码将生成一个包含系统Impulse响应的图形，其中横轴表示时间，纵轴表示响应幅值。通过观察Impulse响应图，我们可以了解系统的响应特性，如上升时间、峰值时间、超调量和调节时间等。

三、实例分析

3.1 系统参数对Impulse响应的影响

为了更好地理解传递函数参数对系统Impulse响应的影响，我们可以对比不同阻尼比ζ下的Impulse响应图。

```matlab

% 定义不同的阻尼比

zeta_values = [0.1, 0.5, 1.0];

% 创建多个传递函数模型并绘制Impulse响应图

figure;

hold on;

for i = 1:length(zeta_values)

zeta = zeta_values(i);

denominator = [1 2*zeta*omega omega^2];

sys = tf(numerator, denominator);

impulse(sys);

hold off;

pause(0.1); % 暂停以可视化每个Impulse响应

hold on;

title('Impulse Response for Different Damping Ratios');

xlabel('Time (s)');

ylabel('Response');

legend({'ζ = 0.1', 'ζ = 0.5', 'ζ = 1.0'}, 'Location', 'Best');

grid on;

end

```

通过比较不同阻尼比下的Impulse响应图，我们可以发现：

当ζ较小时（如0.1），系统响应具有较大的超调量和较长的调节时间，表现为振荡响应。

当ζ增大至中等值（如0.5）时，系统响应的超调量减小，调节时间缩短，系统更加稳定。

当ζ达到1.0时，系统表现为无超调、无振荡的临界阻尼响应。

3.2 系统优化建议

基于Impulse响应图的分析，我们可以提出以下系统优化建议：

减小超调量：通过增加阻尼比ζ，可以减小系统的超调量，使系统响应更加平稳。但需要注意的是，过大的阻尼比可能会导致系统响应速度变慢。

缩短调节时间：调节时间是指系统响应达到并保持在稳态值附近所需的时间。通过调整系统参数（如自然频率ω和阻尼比ζ），可以缩短调节时间，提高系统的响应速度。

避免振荡：对于某些应用，系统的振荡响应是不希望的。通过选择合适的阻尼比ζ，可以避免系统响应中的振荡现象，提高系统的稳定性。

四、其他注意事项

4.1 传递函数模型的准确性

在使用IOTransfer函数创建传递函数模型时，需要确保传递函数的分子和分母多项式系数准确无误。错误的系数可能导致系统响应与实际不符。

4.2 仿真时间的设置

在绘制Impulse响应图时，MATLAB会根据系统的动态特性自动选择合适的仿真时间。但在某些情况下，用户可能需要手动设置仿真时间以更好地观察系统响应。可以使用impulse函数的'Tfinal'参数来指定仿真时间范围。

```matlab

% 设置仿真时间范围

Tfinal = 10; % 仿真时间设为10秒

impulse(sys, Tfinal);

```

4.3 图形的美观性

为了提高图形的可读性和美观性，可以对Impulse响应图进行个性化设置，如调整标题、轴标签、图例和网格等。此外，还可以使用MATLAB的绘图工具进行进一步的美化和标注。

结语

通过本文的介绍，我们了解了如何在MATLAB中使用IOTransfer函数创建传递函数模型并绘制Impulse响应图。通过实例分析和优化建议，我们深入理解了系统参数对Impulse响应的影响，并提出了相应的系统优化策略。在实际应用中，我们应结合具体需求和系统特性，灵活运用MATLAB的控制系统工具箱进行仿真和分析，以实现更加高效和可靠的系统设计。