全等三角形的六种判定条件是什么？

2024-12-05 12:27:11

在几何学中，全等三角形是一个重要的概念，它指的是两个三角形在形状和大小上完全相同。换句话说，如果两个三角形能够完全重合，那么它们就是全等的。为了判断两个三角形是否全等，数学家们总结出了几种判定条件，这些条件为我们提供了一种切实可行的方法来判断和证明三角形之间的相等关系。本文将详细介绍全等三角形的六种判定条件，包括SSS、SAS、ASA、AAS、HL以及定义法。

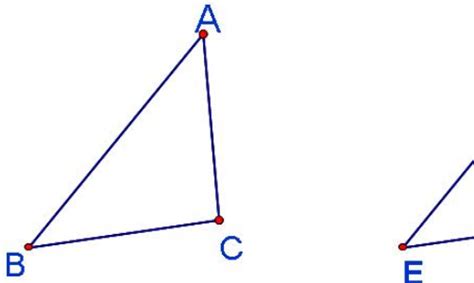
全等三角形的六种判定条件是什么？ 1

SSS（三边相等）

SSS判定条件是指，如果两个三角形的三条边分别相等，那么这两个三角形就是全等的。这是最直接的一种判定方法，因为它只涉及到了三角形的边长。例如，三角形ABC和三角形DEF，如果AB=DE，BC=EF，AC=DF，那么根据SSS条件，我们可以确定三角形ABC和三角形DEF是全等的。

全等三角形的六种判定条件是什么？ 2

SAS（两边和夹角相等）

SAS判定条件是指，如果两个三角形的两边和它们之间的夹角分别相等，那么这两个三角形就是全等的。这个条件涉及到三角形的两边和一个夹角，是几何证明中常用的判定方法之一。例如，三角形ABC和三角形DEF，如果AB=DE，AC=DF，且夹角∠BAC=∠EDF，那么根据SAS条件，我们可以确定三角形ABC和三角形DEF是全等的。

全等三角形的六种判定条件是什么？ 3

ASA（两角和夹边相等）

ASA判定条件是指，如果两个三角形的两个角和它们之间的一条边分别相等，那么这两个三角形就是全等的。这个条件涉及到三角形的两个角和一个夹边，也是几何证明中常用的判定方法之一。例如，三角形ABC和三角形DEF，如果∠BAC=∠EDF，∠ABC=∠EFD，且夹边AC=DF，那么根据ASA条件，我们可以确定三角形ABC和三角形DEF是全等的。

全等三角形的六种判定条件是什么？ 4

AAS（两角和一边对应相等）

AAS判定条件是指，如果两个三角形的两个角和它们之间的另一条边的对应边分别相等，那么这两个三角形就是全等的。这个条件也涉及到三角形的两个角，但与ASA不同的是，AAS条件中的两个角并不是相邻的，而是分别位于三角形的两侧，并且还需要一个对应边相等。例如，三角形ABC和三角形DEF，如果∠BAC=∠EDF，∠ABC=∠EFD，且对应边AB=DE，那么根据AAS条件，我们可以确定三角形ABC和三角形DEF是全等的。

HL（斜边和一条直角边相等）

HL判定条件是指，如果两个直角三角形的一条直角边和斜边分别相等，那么这两个三角形就是全等的。这个条件只适用于直角三角形，是直角三角形特有的判定方法。例如，直角三角形ABC和直角三角形DEF，如果斜边BC=EF，且直角边AC=DF（或另一条直角边AB=DE），那么根据HL条件，我们可以确定直角三角形ABC和直角三角形DEF是全等的。

定义法（完全重合）

除了上述五种判定条件外，还有一种更直观的方法来判断两个三角形是否全等，那就是定义法。根据全等三角形的定义，如果两个三角形能够完全重合，那么它们就是全等的。这种方法虽然直观，但在实际证明中往往需要通过其他判定条件来间接证明两个三角形能够完全重合。

全等三角形的性质

全等三角形具有一系列重要的性质，这些性质在几何证明中经常用到。首先，全等三角形的对应边相等，对应角也相等。这意味着，如果两个三角形是全等的，那么它们的每一条边和每一个角都分别相等。其次，全等三角形的对应边上的高、对应角的角平分线、对应边上的中线也都相等。此外，全等三角形的面积和周长也相等。这些性质为我们提供了判断两个三角形是否全等的重要依据，也为几何证明提供了有力的工具。

注意事项

在使用全等三角形的判定条件时，需要注意以下几点：

1. 判定条件的选择：不同的判定条件适用于不同的情况。在实际证明中，需要根据已知条件选择合适的判定条件。

2. 对应边和对应角的识别：在证明全等三角形时，需要正确识别对应边和对应角。对应边是相等的边，对应角是相等的角。

3. 书写顺序和格式：在书写证明过程时，需要注意书写顺序和格式。通常先写出已知条件，然后根据判定条件逐步推导出结论。

4. 注意SSA和AAA不能判定全等：虽然SSA（两边和非夹角相等）和AAA（三角相等）看起来与某些判定条件相似，但它们并不能用来判定三角形全等。

应用实例

以下是一个应用全等三角形判定条件的实例：

已知三角形ABC和三角形DEF，其中AB=DE，AC=DF，∠BAC=∠EDF。我们需要证明三角形ABC和三角形DEF是全等的。

证明：

1. 根据已知条件，AB=DE，AC=DF，∠BAC=∠EDF。

2. 根据SAS判定条件，如果两个三角形的两边和它们之间的夹角分别相等，那么这两个三角形就是全等的。

3. 因此，我们可以得出三角形ABC和三角形DEF是全等的。

通过这个实例，我们可以看到全等三角形的判定条件在几何证明中的重要作用。它们为我们提供了一种切实可行的方法来判断和证明三角形之间的相等关系。

结语

全等三角形是几何学中一个重要的概念，它涉及到三角形的形状和大小。为了判断两个三角形是否全等，数学家们总结出了几种判定条件，包括SSS、SAS、ASA、AAS、HL以及定义法。这些条件为我们提供了一种切实可行的方法来判断和证明三角形之间的相等关系。在实际应用中，我们需要根据已知条件选择合适的判定条件，并注意对应边和对应角的识别以及书写顺序和格式。通过掌握这些判定条件和性质，我们可以更好地理解和应用全等三角形的知识。