在数学几何学中,全等三角形是一个重要的概念。当我们说两个三角形全等时,意味着这两个三角形的三边和三角都完全相等。了解如何判断两个三角形是否全等,对于解决许多几何问题至关重要。以下是判断全等三角形的几种常用方法。
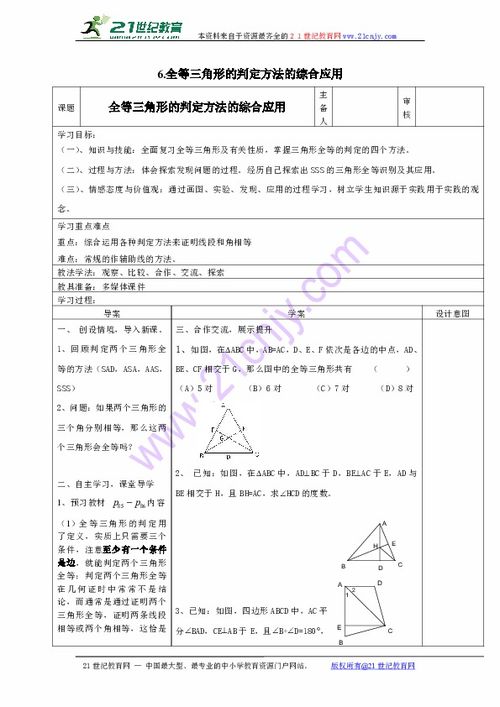
第一种方法是SSS(Side-Side-Side)全等判定。SSS全等判定,也称为边边边全等判定,是指如果两个三角形的三边分别相等,则这两个三角形全等。例如,如果三角形ABC的三边AB、BC和CA分别与三角形DEF的三边DE、EF和FD相等,那么我们可以得出三角形ABC全等于三角形DEF。这种方法非常直观,因为当两个三角形的三边都相等时,它们的形状和大小必然相同。

第二种方法是SAS(Side-Angle-Side)全等判定。SAS全等判定,也称为边角边全等判定,是指如果两个三角形的两边及它们之间的夹角分别相等,则这两个三角形全等。假设三角形ABC的两边AB和BC与三角形DEF的两边DE和EF相等,且夹角∠B等于夹角∠E,那么我们可以确定三角形ABC全等于三角形DEF。SAS全等判定在实际应用中非常常见,比如在测量和构建中,我们经常通过确定两条边和它们之间的夹角来确认两个三角形的全等性。
第三种方法是ASA(Angle-Side-Angle)全等判定。ASA全等判定,也称为角边角全等判定,是指如果两个三角形的两角及它们之间的夹边分别相等,则这两个三角形全等。例如,如果三角形ABC的两角∠A和∠B与三角形DEF的两角∠D和∠E相等,且夹边AB等于夹边DE,那么我们可以得出三角形ABC全等于三角形DEF。ASA全等判定利用了三角形内角和的性质,即三角形的三个内角之和等于180度,因此当两个三角形的两个角和夹边相等时,第三个角也必然相等,从而确保三角形的全等。
第四种方法是AAS(Angle-Angle-Side)全等判定。AAS全等判定,也称为角角边全等判定,是指如果两个三角形的两角及非夹边分别相等,则这两个三角形全等。比如,如果三角形ABC的两角∠A和∠C与三角形DEF的两角∠D和∠F相等,且非夹边BC等于非夹边EF,那么我们可以确认三角形ABC全等于三角形DEF。AAS全等判定与ASA全等判定类似,但区别在于AAS涉及的是两个角和一条非夹边,而不是夹边。在证明AAS全等时,我们通常需要利用三角形内角和的性质来找出第三个相等的角,从而确认三角形的全等性。
第五种方法是HL(Hypotenuse-Leg)全等判定,这是直角三角形特有的全等判定方法。HL全等判定,也称为斜边直角边全等判定,是指如果两个直角三角形的斜边和一条直角边分别相等,则这两个直角三角形全等。例如,在直角三角形ABC和直角三角形DEF中,如果斜边AC等于斜边DF,且直角边AB等于直角边DE,那么我们可以得出直角三角形ABC全等于直角三角形DEF。HL全等判定利用了直角三角形的性质,即直角三角形的斜边和一条直角边唯一确定一个直角三角形。
在判断三角形全等时,选择哪种方法取决于已知条件。如果我们知道三角形的三边长度,可以使用SSS全等判定;如果我们知道两边和它们之间的夹角,可以使用SAS全等判定;如果我们知道两角和它们之间的夹边,可以使用ASA全等判定;如果我们知道两角和非夹边,可以使用AAS全等判定;如果我们在处理直角三角形,并且知道斜边和一条直角边,则可以使用HL全等判定。
值得注意的是,虽然全等三角形的判定方法有五种,但在实际应用中,我们并不需要总是逐一尝试每一种方法。通过仔细观察和分析题目给出的条件,我们通常可以快速确定最适合的判定方法。此外,全等三角形的判定方法并不是孤立的,它们之间存在内在的联系。例如,在证明SAS全等时,我们可能会用到三角形内角和的性质,这与ASA全等判定有关;在证明AAS全等时,我们也可能需要利用SAS或SSS全等判定来找到额外的相等条件。
在解决与全等三角形相关的问题时,除了熟练掌握全等三角形的判定方法外,我们还需要注意以下几点:首先,要确保题目给出的条件足够支持我们使用某种全等判定方法;其次,在证明过程中要严格遵守逻辑推理规则,避免出现逻辑错误;最后,在得出结论后,要仔细检查答案是否符合题目的要求。
总之,判断全等三角形的方法包括SSS、SAS、ASA、AAS和HL五种。这些方法在数学几何学中具有广泛的应用,是解决许多几何问题的关键。通过熟练掌握这些方法,我们可以更加准确地判断两个三角形是否全等,并在实际问题中灵活运用这些判定方法来解决各种几何问题。同时,我们也要注意在证明过程中严格遵守逻辑推理规则,确保答案的正确性和可靠性。
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2