在数学的广阔天地里,有一个既实用又有趣的概念——最小公倍数(Least Common Multiple, LCM)。简单来说,两个或多个整数的最小公倍数,就是它们共同的倍数中最小的一个。这个概念在日常生活中并不显眼,但在解决时间、分组、资源分配等问题时,却常常扮演着关键角色。那么,我们该如何找到两个数的最小公倍数呢?接下来,就让我们一起踏上这场探索之旅。

首先,我们要明确几个基础概念:倍数、公倍数和最小公倍数。
倍数:一个数能够被另一个数整除,那么这个数就是另一个数的倍数。比如,6是3的倍数,因为6除以3没有余数。
公倍数:两个或多个整数共有的倍数。比如,4和6的公倍数有12、24、36...等。
最小公倍数:在所有的公倍数中,最小的一个就是最小公倍数。对于4和6来说,它们的最小公倍数是12。
对于较小的数,我们可以直接通过列举法来找到它们的最小公倍数。这种方法虽然简单直接,但效率不高,适合用于教学演示或处理小数字的情况。
步骤:
1. 列出第一个数的所有倍数。
2. 在这些倍数中,找出同时也是第二个数的倍数的数。
3. 这些共同的倍数中,最小的那个就是最小公倍数。
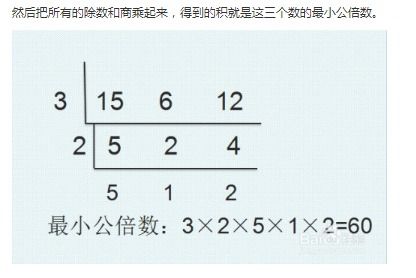
示例:求12和15的最小公倍数。
列出12的倍数:12, 24, 36, 48, 60...
找出同时是15的倍数的数:在这些数中,24不是15的倍数,但30(注意,这里直接跳到了下一个可能的公倍数,因为24之后很快就是30了,实际上在列举时应逐一检查)是。
因此,12和15的最小公倍数是30。
对于较大的数,或者想要更高效地求解最小公倍数时,我们可以采用分解质因数的方法。这种方法基于一个数学原理:两个数的乘积等于它们的最大公约数(Greatest Common Divisor, GCD)与最小公倍数的乘积。
步骤:
1. 将两个数分别分解为质因数。
2. 对于每个质因数,取它在两个数中出现次数最多的那个次数。
3. 将这些质因数相乘,得到的结果就是最小公倍数。
示例:求60和48的最小公倍数。
分解质因数:
60 = 2^2 × 3 × 5
48 = 2^4 × 3
取每个质因数出现次数的最大值:
2的最大次数是4(来自48)
3的最大次数是1(两者都是)
5的最大次数是1(仅来自60)
相乘得到最小公倍数:2^4 × 3 × 5 = 240
由于前面提到的数学原理,我们还可以利用两个数的最大公约数来快速求解最小公倍数。这种方法在已知两数最大公约数的情况下尤为方便。
公式:两数的乘积 = 两数的最大公约数 × 两数的最小公倍数
步骤:
1. 首先求出两数的最大公约数(可以使用辗转相除法等方法)。
2. 将两数的乘积除以它们的最大公约数,得到的结果就是最小公倍数。
示例:已知60和48的最大公约数是12,求它们的最小公倍数。
使用公式:LCM(60, 48) = (60 × 48) ÷ 12
计算得:LCM(60, 48) = 240
了解了如何求解最小公倍数后,我们不难发现它在日常生活中的广泛应用。比如:
时间规划:当需要安排两个不同周期的活动时,知道它们的最小公倍数可以帮助我们找到两个活动同时进行的最佳时间点。
资源分配:在分配有限资源给不同需求的群体时,利用最小公倍数可以确保资源被公平且高效地利用。
学习分组:在需要将学生分成若干小组,且每组人数需满足两个不同条件时,最小公倍数可以帮助我们确定最合适的分组人数。
通过上述介绍,我们不难发现,求解两个数的最小公倍数并非难事,关键在于掌握正确的方法和技巧。无论是通过直观的列举法,
 状元搭档类型:学习办公
状元搭档类型:学习办公状元搭档是一款专为学习者和职场人士设计的高效学习与管理工具,...
 Tentacle locker 游戏类型:冒险解谜
Tentacle locker 游戏类型:冒险解谜Tentacle locker 游戏简介 Tentacle...
 指趣游戏盒最新版类型:实用工具
指趣游戏盒最新版类型:实用工具指趣游戏盒最新版是一款专为游戏爱好者打造的应用软件,旨在为用...
 逸乘车主司机端app类型:生活服务
逸乘车主司机端app类型:生活服务逸乘车主司机端是一款专为车主和司机设计的出行服务应用,旨在提...
 末日方舟无限资源类型:冒险解谜
末日方舟无限资源类型:冒险解谜末日方舟无限资源简介 《末日方舟无限资源》是一款融合了策略...
88.74M撕歌 5.91.1版本
59.62M绿色地狱1.3.3
93.43Mwifi万能钥匙国际版显密码
107.19M小熊倒数
187.07M潮汐守望者战力无限制版
45.34M尘柚漫画官方
40.45M栗子漫画软件
70.96M希象传屏
134.18Mbobo浏览器无国界全球版
37.81M重装机兵安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2