矩阵的乘法运算,作为线性代数中的核心概念之一,不仅是数学研究的重要工具,更是计算机科学、物理学、工程学等多个领域不可或缺的一部分。它以一种简洁而强大的方式,描述了多维空间中的线性变换,为解决复杂问题提供了有力的数学手段。本文将从定义与基本性质、计算步骤与示例、几何意义与应用,以及与其他数学概念的关联等多个维度,深入探讨矩阵乘法的奥秘。
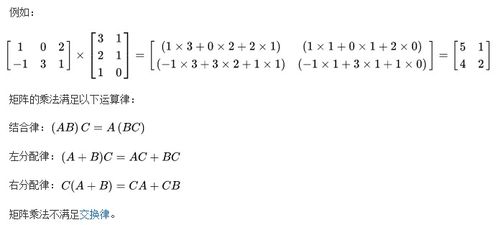
矩阵乘法,简而言之,就是两个矩阵按照一定规则相乘得到一个新的矩阵的过程。若A为m×n矩阵(即m行n列),B为n×p矩阵,则它们的乘积C=AB是一个m×p矩阵。具体地,C中的元素c_ij等于A的第i行与B的第j列对应元素乘积之和。这个定义看似简单,却蕴含着丰富的数学结构和性质。

1. 不满足交换律:一般来说,矩阵乘法不满足交换律,即AB≠BA,除非满足特定条件(如两者为方阵且可交换)。

2. 满足分配律:矩阵乘法满足左、右分配律,即A(B+C)=AB+AC,(B+C)A=BA+CA。
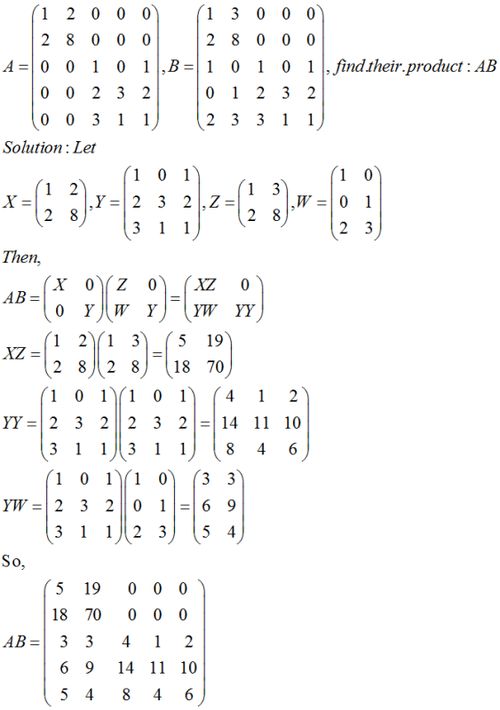
3. 单位矩阵:对于任何矩阵A,存在一个单位矩阵I(对角线为1,其余为0的方阵),使得AI=IA=A。单位矩阵在矩阵乘法中扮演着类似于实数乘法中1的角色。
4. 零矩阵:任何矩阵与零矩阵相乘结果为零矩阵,即A0=0,0A=0,其中0表示零矩阵。
理解矩阵乘法的关键在于掌握其计算步骤。以下是一个具体的计算示例,旨在直观展示这一过程。
假设有两个矩阵A和B:
A = \[\[1, 2],
\[3, 4]]
B = \[\[5, 6],
\[7, 8]]
计算AB的过程如下:
1. 确定结果矩阵C的维度。由于A是2×2矩阵,B也是2×2矩阵,所以C将是2×2矩阵。
2. 对于C中的每个元素c_ij,计算A的第i行与B的第j列对应元素乘积之和。
c_11 = 1×5 + 2×7 = 5 + 14 = 19
c_12 = 1×6 + 2×8 = 6 + 16 = 22
c_21 = 3×5 + 4×7 = 15 + 28 = 43
c_22 = 3×6 + 4×8 = 18 + 32 = 50
因此,C = AB = \[\[19, 22],
\[43, 50]]
矩阵乘法不仅仅是一种抽象的代数运算,它还具有深刻的几何意义。在线性代数中,矩阵可以视为对向量空间进行线性变换的工具。具体而言,一个m×n矩阵A可以看作是从n维空间到m维空间的一个线性映射。矩阵乘法AB则代表了先进行B代表的变换,再进行A代表的变换的复合变换。
这一几何解释在图形学、物理学、计算机科学等领域有着广泛的应用。例如,在计算机图形学中,通过矩阵乘法可以方便地实现图形的缩放、旋转、平移等变换;在物理学中,量子力学中的态矢量和算符常通过矩阵表示,矩阵乘法描述了物理过程的演变;在机器学习领域,矩阵乘法是神经网络前向传播和反向传播算法的基础,用于计算权重更新和输出预测。
矩阵乘法不仅是线性代数的基础,还与众多数学概念紧密相连,形成了数学理论体系中一张错综复杂但又井然有序的网络。
1. 行列式:矩阵乘法的结果矩阵的行列式等于原矩阵行列式的乘积,即|AB|=|A|×|B|。这一性质在求解线性方程组、判断矩阵可逆性等方面具有重要意义。
2. 特征值与特征向量:若A是一个方阵,λ是A的一个特征值,x是对应的特征向量,则有Ax=λx。矩阵乘法在特征值与特征向量的计算中起着关键作用,它们共同揭示了矩阵的固有性质,如对称性、正定性等。
3. 线性变换与矩阵表示:任何线性变换都可以通过矩阵来表示,而矩阵乘法则是这些变换复合的运算方式。这一联系不仅加深了我们对线性变换的理解,也为解决复杂问题提供了强有力的数学工具。
4. 奇异值分解(SVD)与特征值分解(EVD):这些分解方法都是基于矩阵乘法的,它们允许我们将矩阵分解为更简单的组成部分,从而揭示矩阵的内在结构和性质。SVD在信号处理、图像压缩等领域有着广泛应用,而EVD则在统计学、机器学习等领域发挥着重要作用。
5. 矩阵群与线性群:在更抽象的层面上,矩阵乘法构成了矩阵群和线性群的基础。这些群论概念不仅在数学内部有着深远的理论意义,而且在密码学、量子计算等领域也展现出巨大的应用潜力。
综上所述,矩阵的乘法运算不仅是线性代数中的一个基本概念,更是连接数学与现实世界的桥梁。它以其独特的数学魅力,跨越了学科界限,成为众多领域不可或缺的数学工具。通过对矩阵乘法的深入研究,我们不仅能够更好地理解和解决具体问题,还能够领略到数学之美,感受到它对人类文明进步的推动作用。
19.95M海星tv官方版
110.34M洛雪音乐安卓版
85.14M昭凌画质助手
28.94M漫哇免费版漫画阅读
64.43M海虎一百万匹
77.55M明星大厨2游戏手机版
2.12M搜番app正版
103.25M优获云扫码点餐app
60.23M搜书神器
94.54M纸牌动物园星球
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2