如何进行除法通用竖式计算？

除法通用竖式计算是数学学习中的一项基本技能，它能够帮助我们更直观地理解和解决除法问题。下面，我们就来详细探讨一下除法通用竖式计算的具体步骤和技巧。

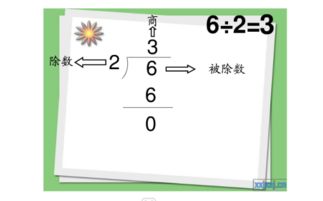
首先，我们需要明确除法的基本概念。除法是四则运算之一，表示将一个数（被除数）分成若干等份，每份的数量就是商，可能还有剩余的部分，称为余数。在进行除法竖式计算时，我们通常会将这个过程分解为几个步骤，以便更清晰地看出每一步的计算结果。

在进行除法竖式计算之前，我们需要准备好纸笔，并确定好被除数、除数和商的位置。一般来说，我们会将被除数写在竖式的上方，除数写在左侧，然后在被除数下方逐步写出商和余数。接下来，我们就可以开始具体的计算过程了。

第一步，我们需要确定商的位数。这通常是通过比较被除数和除数的大小来完成的。如果被除数的位数比除数多，那么商的位数就会比被除数少一位；如果被除数的位数与除数相同或比除数少，那么商的位数就需要通过试商来确定。试商的过程是逐步猜测商的每一位数字，然后通过与除数相乘来验证猜测是否正确。

第二步，我们开始进行具体的除法运算。首先，我们将被除数的最高位数字（如果被除数是多位数的话）除以除数，得到的结果就是商的最高位数字。然后，我们将这个商的最高位数字与除数相乘，得到的结果写在被除数的下方，并与被除数的下一位数字对齐。接下来，我们将被除数的这个部分（即已经除以过的部分和下一位数字组成的数）减去刚刚得到的乘积，得到的差就是余数。

第三步，我们继续用余数去除以除数，得到的结果就是商的下一位数字。然后，我们再将这个新的商的数字与除数相乘，得到的结果写在余数的下方，并与被除数的下一位数字（如果有的话）对齐。同样地，我们将这个新的部分减去乘积，得到新的余数。

这个过程会一直重复下去，直到被除数被完全除尽或者不能再继续除下去为止。如果被除数被完全除尽了，那么最后的余数就是0；如果不能再继续除下去，那么最后的余数就是除不尽的部分，也就是余数。

在进行除法竖式计算时，我们需要注意以下几点：

一是要确保每一步的计算都准确无误。因为除法运算是一个连续的过程，如果某一步计算错误了，那么后面的计算结果都会受到影响。因此，在进行除法竖式计算时，我们需要特别小心，确保每一步都计算正确。

二是要注意商的位数和余数的处理。商的位数需要根据被除数和除数的大小来确定，而余数则需要作为下一步计算的被除数的一部分继续参与运算。如果忽略了这一点，就可能导致计算错误。

三是要学会利用除法竖式计算的技巧来简化计算过程。例如，我们可以通过试商来快速确定商的每一位数字；我们还可以通过观察被除数和除数的特点来选择更合适的计算方法；我们还可以利用一些已知的运算规律来简化计算过程等。

除法竖式计算不仅在数学学习中有着广泛的应用，而且在实际生活中也有着重要的作用。例如，我们在购物时需要计算商品的单价和总价；我们在制作食物时需要按照比例来分配原料；我们在进行科学实验时需要精确测量和计算等。这些都需要用到除法竖式计算的知识和技能。

此外，除法竖式计算还是进一步学习数学的基础。在学习更高级的数学知识时，我们往往需要用到除法竖式计算来求解一些问题。因此，掌握除法竖式计算的方法和技巧对于我们未来的学习和工作都是非常重要的。

当然，在学习除法竖式计算的过程中，我们可能会遇到一些困难和挑战。例如，我们可能会发现试商的过程比较繁琐和耗时；我们可能会因为粗心大意而犯一些计算错误；我们可能会因为对除法的概念理解不够深入而难以掌握竖式计算的方法等。但是，只要我们保持耐心和毅力，不断练习和巩固所学知识，就一定能够克服这些困难和挑战。

总之，除法通用竖式计算是一项非常重要的数学技能。它不仅能够帮助我们解决日常生活中的实际问题，还能够为我们进一步学习数学打下坚实的基础。因此，我们应该认真学习除法竖式计算的方法和技巧，不断提高自己的计算能力和数学素养。同时，我们还应该注重实践和应用所学知识，将理论知识与实际生活相结合起来，以便更好地掌握和运用这项技能。