在我们日常的数学学习和生活中,经常会听到“有理数”这个词。那么,有理数到底是什么意思呢?它涵盖了哪些具体的数字呢?今天,我们就来一起揭开有理数的神秘面纱,让它变得通俗易懂。
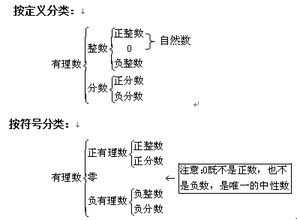
首先,我们来明确一下有理数的定义。有理数,顾名思义,就是“有道理”的数。这里的“道理”其实是指这些数都可以表示成两个整数的比(分数)形式。换句话说,有理数是可以被精确表示的,不会有无穷无尽的小数位。具体来说,如果两个整数a和b(b不等于0)相除,得到的商就是有理数,记作a/b。

了解了定义之后,我们来看看哪些常见的数属于有理数。

首先,最简单也最直接的一类有理数就是整数。整数包括正整数(如1, 2, 3,...)、零和负整数(如-1, -2, -3,...)。这些整数都可以看作是分母为1的分数,例如整数3可以写成3/1,因此整数是有理数的一个子集。

除了整数之外,有理数还包括分数。分数可以是正的,也可以是负的。例如,1/2和-3/4都是有理数。这里需要注意的是,即使分数的分子和分母都是负数,最终得到的结果仍然是有理数,只不过正负号会根据分子和分母的符号来确定。例如,-1/-2等于1/2,结果为正有理数。
另一个帮助我们理解有理数的重要特征是,有理数都可以表示为有限小数或无限循环小数。有限小数是指小数点后只有有限位数字的数,比如0.5、1.25和7.333。无限循环小数是指小数点后某一段数字无限重复的数,比如1/3等于0.333...,其中3无限循环。
为了更好地理解有理数,让我们通过一些具体的例子来加以说明。
0.75:这是一个有限小数,可以表示为3/4,因此是有理数。
1.666...(6无限循环):这是一个无限循环小数,可以表示为5/3,因此也是有理数。
2/3:这是一个负分数,可以转换为小数形式-0.666...,其中6无限循环,因此也是有理数。
0:这是整数,可以看作是0/1或任何形式a/a(a不等于0),因此也是有理数。
有理数的另一个特点是,它们支持基本的算术运算,包括加法、减法、乘法和除法(除数不为零)。这些运算的结果仍然是有理数。例如:
加法:1/2 + 1/4 = 2/4 + 1/4 = 3/4
减法:3/4 - 1/2 = 3/4 - 2/4 = 1/4
乘法:1/3 * 2/5 = 2/15
除法:2/3 ÷ 1/4 = 2/3 * 4/1 = 8/3
为了更全面地理解有理数,我们还需要知道它与无理数的区别。无理数是指那些无法表示为两个整数之比的数,即无法写成分数形式的数。无理数的小数部分是无限不循环的。最常见的无理数包括圆周率π(约等于3.14159...)和自然对数的底数e(约等于2.71828...)。此外,像根号2、根号3等无法开方得到整数的平方根也是无理数。
有理数不仅在数学学科中占据重要地位,而且在我们的日常生活中也有着广泛的应用。例如,我们在购物时计算折扣、分配食物时的比例、设置闹钟的时间以及量度物体的尺寸时,都会用到有理数。
购物:假设一件原价100元的商品打七折,那么折扣后的价格就是70元。这里的七折可以用有理数0.7来表示。
烹饪:当你需要按照食谱将食材分成三份时,每一份的比例就是1/3,这也是有理数。
时间:当我们设定闹钟为6点30分时,这个时间点可以用有理数6.5小时(将分钟转换为小时的小数形式)来表示。
测量:当我们用尺子测量一个物体的长度为1.5厘米时,这也是有理数。
在数学中,有理数不仅限于十进制形式,它们还可以在二进制、八进制和十六进制等不同的数制中表示。虽然
 死亡战车2游戏安卓版类型:赛车竞速
死亡战车2游戏安卓版类型:赛车竞速《死亡战车2》是一款充满刺激与惊险的赛车竞速游戏,专为热爱速...
 lsplibrary类型:拍摄美化
lsplibrary类型:拍摄美化LSPLibrary(LISP库)是一款专为程序员和开发者设...
 英雄角斗场无敌修改版类型:动作格斗
英雄角斗场无敌修改版类型:动作格斗《英雄角斗场无敌修改版》是一款融合了策略与角色扮演元素的竞技...
 王牌战机无限钻石版类型:飞行射击
王牌战机无限钻石版类型:飞行射击王牌战机无限钻石版是一款结合飞行射击与策略战术的顶级空战游戏...
 豆豆计算器最新版类型:实用工具
豆豆计算器最新版类型:实用工具豆豆计算器最新版是一款专为日常计算需求设计的手机计算器应用,...
36.05MAI文案师
103.99M绘分享最新版
78.40M好玩部落抓娃娃
423.10M月影别墅官方下载
2.50M游戏重复名生成器app
108.85M绘本树
114.80M精灵工具箱免费版
27.10M美蓝漫画正版
32.89M河北电动自行车登记系统app
48.82M旗星影视软件官方版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2