在数学的世界里,一元二次方程占据了极其重要的地位。它不仅是初中数学课程的核心内容,也是高中数学乃至更高级别数学学科的重要基础。一元二次方程的形式通常为ax²+bx+c=0(其中a≠0),这样的方程在解决实际问题时具有广泛的应用,比如物理中的抛体运动、经济学中的成本收益分析等。而在研究一元二次方程的过程中,了解其顶点坐标显得尤为重要,因为顶点坐标不仅可以帮助我们直观地理解方程的图像,还能在解决某些问题时提供极大的便利。
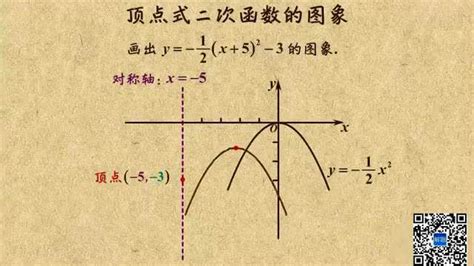
一元二次方程的顶点坐标公式是解决这一问题的关键。简单来说,顶点坐标公式能够让我们直接找出一元二次方程图像的最高点(或最低点)的位置,这对于分析方程的性质和解决实际问题都至关重要。那么,一元二次方程的顶点坐标公式具体是什么呢?

一元二次方程的顶点坐标公式可以表示为:(-b/(2a), c-b²/(4a))。这个公式是如何得出的呢?我们可以从一元二次方程的标准形式ax²+bx+c=0出发,通过配方的方法将其转化为顶点式。配方是一种数学技巧,它可以将二次方程转化为一个完全平方的形式,从而更容易地找出方程的顶点坐标。

具体来说,我们可以将一元二次方程ax²+bx+c=0(a≠0)改写为a(x²+(b/a)x)+c=0,然后为了完成配方,我们在等式两边同时加上(b/2a)²-c/a,得到a(x²+(b/a)x+(b/2a)²-(b/2a)²)+c+b²/(4a)-c=0,即a(x+(b/2a)²)=(b²-4ac)/(4a)。当a>0时,抛物线开口向上,顶点为最小值点;当a<0时,抛物线开口向下,顶点为最大值点。此时,我们可以将等式两边同时除以a,得到(x+(b/2a))²=(b²-4ac)/(4a²),即(x-(-b/2a))²=((b²-4ac)/a²)/4。进一步化简,我们得到(x-(-b/2a))²=((b/2a)²-c/a),这就是一元二次方程的顶点式。

从顶点式中,我们可以直接读出一元二次方程的顶点坐标。其中,x坐标是-b/(2a),y坐标是c-b²/(4a)。这就是一元二次方程的顶点坐标公式。通过这个公式,我们可以快速找出一元二次方程图像的顶点位置,进而分析方程的性质。

一元二次方程的顶点坐标公式在实际应用中具有广泛的应用。比如,在物理学中,我们常常需要研究抛体运动的轨迹,而抛体运动的轨迹通常可以看作是一个一元二次方程的图像。此时,我们可以通过求解一元二次方程的顶点坐标公式,来找出抛体运动的最高点或最低点的位置,这对于分析抛体运动的性质和解决实际问题都非常重要。
此外,在经济学中,我们也常常需要用到一元二次方程的顶点坐标公式。比如,在研究成本收益分析时,我们可能需要求解一个表示成本或收益与产量之间关系的一元二次方程。此时,我们可以通过求解一元二次方程的顶点坐标公式,来找出成本或收益的最大值或最小值点,这对于制定最优的生产计划和决策具有重要的指导意义。
除了在实际问题中的应用外,一元二次方程的顶点坐标公式在数学学科内部也具有重要的意义。它不仅可以帮助我们更好地理解一元二次方程的性质和图像特征,还可以作为求解一元二次方程根的一种辅助手段。因为在一元二次方程的图像上,顶点坐标与方程的根之间存在一定的关系。通过观察和分析顶点坐标的位置和性质,我们可以对一元二次方程的根做出一些初步的预测和判断。
当然,在学习和应用一元二次方程的顶点坐标公式时,我们也需要注意一些问题。首先,要确保公式中的各个参数都正确无误地代入到公式中。因为公式中的每一个参数都对应着方程中的一个具体项,如果参数代入错误,就会导致计算结果出现偏差。其次,要注意公式的适用范围和限制条件。虽然一元二次方程的顶点坐标公式在大多数情况下都适用,但在某些特殊情况下(比如当a=0时),公式就不再适用。因此,在使用公式时,我们需要根据具体情况进行判断和选择。
总之,一元二次方程的顶点坐标公式是解决一元二次方程相关问题的重要工具。它不仅可以帮助我们快速找出一元二次方程图像的顶点位置,还可以作为求解一元二次方程根的一种辅助手段。在学习和应用这个公式时,我们需要充分理解其背后的数学原理和推导过程,并注意公式的适用范围和限制条件。只有这样,我们才能更好地掌握这个工具,并灵活运用它来解决实际问题。
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2