四面体体积计算公式详解

在三维几何学中，四面体是一种具有四个面、四个顶点以及六条棱的简单多面体。其体积的计算是几何学中的一个基本问题，不仅在理论上具有重要意义，而且在实际应用中也有广泛需求，如地质学、工程学以及计算机图形学等领域。本文旨在介绍四面体体积的计算公式，并探讨其推导过程和相关应用，以提高读者对四面体体积计算的理解。

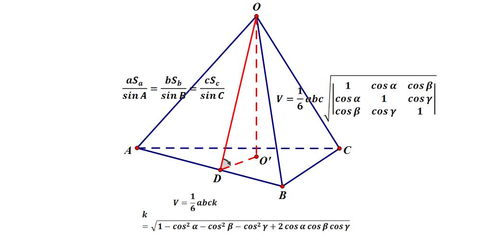
四面体的体积计算公式可以通过多种方式推导得出，其中最著名的是利用向量的混合积方法。在三维空间中，任意三个不共线的向量a、b、c可以形成一个平行六面体，该平行六面体的体积V可以通过向量a、b、c的混合积来计算，即V=a·(b×c)。当这三个向量所构成的平行六面体的一个顶点与原点重合时，该平行六面体便退化为一个四面体，其体积恰好为平行六面体体积的1/6。

具体地，设四面体的四个顶点分别为A(x1, y1, z1)、B(x2, y2, z2)、C(x3, y3, z3)和D(x4, y4, z4)，则向量AB、AC和AD可以分别表示为B-A、C-A和D-A。根据向量混合积的定义，有

AB×AC = (y2-y1)(z3-z1)i - (x2-x1)(z3-z1)j + (x2-x1)(y3-y1)k - [(y2-y1)(z3-z1)-(x2-x1)(y3-y1)]的对应分量乘以单位向量i、j、k后得到的向量，

其中i、j、k分别为x、y、z轴上的单位向量。接下来，计算向量AD与向量AB×AC的点积，即

AD·(AB×AC) = [(x4-x1)i + (y4-y1)j + (z4-z1)k]·[AB×AC的对应分量]，

该点积的结果即为四面体体积的6倍。因此，四面体的体积V可以表示为

V = 1/6 |AD·(AB×AC)| = 1/6 |(x4-x1)[(y2-y1)(z3-z1)-(x2-x1)(y3-y1)] + (y4-y1)[(x2-x1)(z3-z1)-(y2-y1)(x3-x1)] + (z4-z1)[(x2-x1)(y3-y1)-(y2-y1)(x3-x1)]|。

这个公式是四面体体积计算的基础，它简洁明了地表达了四面体体积与顶点坐标之间的关系。在实际应用中，只需要将四面体的顶点坐标代入公式，即可快速计算出四面体的体积。

除了向量混合积方法外，四面体的体积还可以通过其他方式推导得出。例如，可以利用三棱锥的体积公式，即三棱锥的体积等于底面积乘以高再除以3。在四面体中，可以选择任意一个面作为底面，然后计算该面到其他顶点的距离（即高），最后利用三棱锥的体积公式求出四面体的体积。然而，这种方法相对于向量混合积方法来说，计算过程更为复杂，且需要额外的几何信息（如底面的面积和高）。

此外，还有一种利用行列式计算四面体体积的方法。该方法将四面体的顶点坐标构成一个4×3的矩阵，然后计算该矩阵的行列式，并将结果除以6即可得到四面体的体积。这种方法虽然理论上可行，但在实际应用中计算量较大，且不如向量混合积方法直观易懂。

四面体体积的计算在多个领域都有广泛应用。在地质学中，四面体体积的计算可以用于估计矿体的储量；在工程学中，四面体体积的计算可以用于计算结构的体积和重量；在计算机图形学中，四面体体积的计算可以用于三维模型的生成和处理等。因此，掌握四面体体积的计算方法对于从事相关领域工作的人员来说具有重要的实际意义。

值得注意的是，虽然四面体体积的计算公式相对简单，但在实际应用中仍需注意一些细节问题。例如，在计算过程中需要确保输入的顶点坐标准确无误；在选择计算方法时需要根据具体情况选择最适合的方法；在计算结果中需要注意单位换算和精度控制等问题。这些细节问题的处理对于确保计算结果的准确性和可靠性至关重要。

综上所述，四面体体积的计算是三维几何学中的一个基本问题，具有广泛的应用价值。通过掌握四面体体积的计算公式和推导方法，我们可以更好地理解和应用这一几何概念，为解决实际问题提供有力的数学工具。同时，我们也需要注意在实际应用中处理好各种细节问题，以确保计算结果的准确性和可靠性。希望本文能够帮助读者更好地理解四面体体积的计算方法和相关应用，为学习和工作提供有益的参考。