轻松学会！三角形面积的计算方法

在计算几何学中，三角形作为最基础的多边形之一，其面积的计算是众多数学和工程应用中的核心环节。无论是测量土地面积、设计建筑布局，还是解决物理、计算机图形学中的问题，掌握三角形面积的计算方法都至关重要。那么，三角形面积究竟如何计算呢？以下将详细介绍几种常见且实用的方法。

方法一：底乘以高再除以二

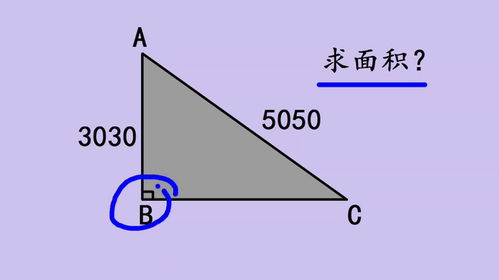
这是计算三角形面积最基本也是最广为人知的方法，源自海伦公式的简化形式。其原理是将三角形视为一个以底边为基，高为垂直距离的矩形的一半。具体步骤为：

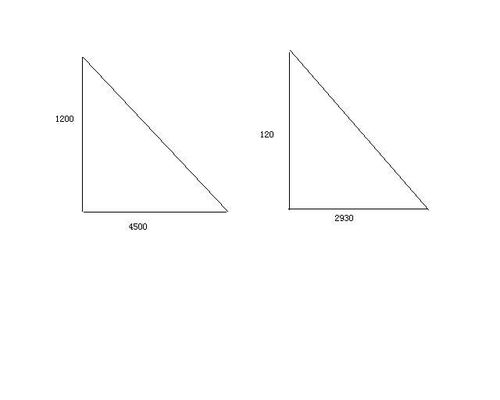
1. 确定底边和高：首先，需要确定三角形的任意一边作为底边，并找到从该边顶点的垂线，这条垂线即为三角形的高。注意，底边和高是互相垂直的。

2. 应用公式：三角形的面积 $A$ 可以通过公式 $A = \frac{1}{2} \times \text{底} \times \text{高}$ 来计算。这里的“底”代表你选择的底边长度，“高”则是垂直于该底边且从顶点到该边的垂线段的长度。

方法二：海伦公式

当三角形的三边长度已知，但无法直接确定底和高时，可以使用海伦公式来计算面积。海伦公式是由古希腊数学家海伦在他的著作《度量论》中首次给出的，适用于任意三角形。

1. 计算半周长：首先，计算三角形三边之和的一半，即 $s = \frac{a + b + c}{2}$，其中 $a$、$b$、$c$ 是三角形的三边长度。

2. 应用海伦公式：然后，使用公式 $A = \sqrt{s(s-a)(s-b)(s-c)}$ 来计算三角形的面积。这个公式巧妙地将三角形的三边长度与面积联系起来，无需知道底和高。

方法三：利用三角函数

在知道三角形两个角的度数和夹在这两个角之间的一边长度时，也可以利用三角函数来计算面积。这通常涉及到正弦、余弦或正切函数。

1. 确定已知条件：假设已知角 $A$、角 $B$（或它们的补角）和边 $c$（对应角 $A$ 和 $B$ 的夹边）。

2. 选择适合的公式：

如果知道两边及其夹角，如 $a$、$b$ 和 $\angle C$，则面积 $A = \frac{1}{2}ab\sin C$。

也可以通过已知角和邻边利用正弦定理转化为边长与角度的乘积，再应用上述公式。

方法四：坐标法

对于平面直角坐标系中的三角形，如果已知其三个顶点的坐标，可以利用坐标法计算面积。这种方法基于行列式和向量外积的概念。

1. 记录顶点坐标：设三角形的三个顶点分别为 $A(x_1, y_1)$，$B(x_2, y_2)$，$C(x_3, y_3)$。

2. 计算面积：利用行列式 $A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|$ 或通过向量外积 $A = \frac{1}{2} \left| \vec{AB} \times \vec{AC} \right|$ 来计算面积。这两种方法本质上是一致的，都是基于三角形两边向量外积的模的一半等于三角形面积的原理。

实际应用中的选择

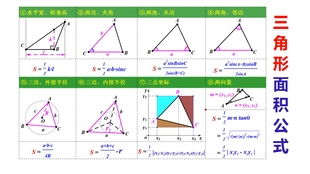
在实际应用中，选择哪种方法计算三角形面积取决于你所拥有的信息。如果知道底和高，直接使用第一种方法最简便；若三边长度已知，则海伦公式是首选；在涉及角度和边长时，可以考虑使用三角函数法；而对于坐标明确的三角形，坐标法提供了一种高效准确的解决方案。

通过理解和掌握这些计算三角形面积的方法，我们不仅能够解决日常学习和工作中的具体问题，还能更加深入地理解几何学中的基本概念和原理。