如何在函数图像上区分并划分第一、第二、第三、第四象限？

在数学中，函数图像是研究函数性质与变化规律的重要工具。当我们提及在函数图像上划分1234象限时，实际上是在平面直角坐标系这一背景下进行的。平面直角坐标系由两条互相垂直且交点为原点的数轴（横轴称为x轴，纵轴称为y轴）组成，它们将平面分为四个部分，即我们通常所说的第一象限、第二象限、第三象限和第四象限。以下将从多个维度深入探讨函数图像在这四个象限中的表现与特性。

一、坐标系基础与象限定义

首先，明确坐标系的基本结构和象限的划分标准至关重要。在平面直角坐标系中，x轴的正半轴向右延伸，负半轴向左延伸；y轴的正半轴向上延伸，负半轴向下延伸。坐标系的原点（0,0）是两条坐标轴的交点。根据点的横纵坐标的正负性，平面被划分为四个区域：

第一象限：所有x坐标和y坐标都为正的点组成的区域。

第二象限：所有x坐标为负、y坐标为正的点组成的区域。

第三象限：所有x坐标和y坐标都为负的点组成的区域。

第四象限：所有x坐标为正、y坐标为负的点组成的区域。

二、函数图像在象限内的分布

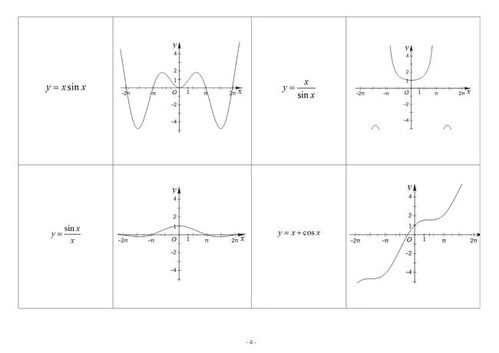
不同类型的函数图像在平面直角坐标系中的表现各异，其穿越或停留在不同象限的方式也各不相同。

1. 线性函数

线性函数（形如y=kx+b，其中k和b为常数，k≠0）的图像是一条直线。直线的位置取决于斜率k和截距b的值。

当k>0且b>0时，直线从第三象限穿过原点进入第一象限。

当k>0且b<0时，直线从第四象限穿过原点进入第一象限。

当k<0且b>0时，直线从第二象限穿过原点进入第四象限。

当k<0且b<0时，直线从第二象限穿过第三象限。

2. 二次函数

二次函数（形如y=ax^2+bx+c，其中a≠0）的图像是一个抛物线。其开口方向、顶点位置及与坐标轴的交点决定了它在哪些象限内可能出现。

当a>0时，抛物线开口向上，可能穿过第一、第二象限（或仅在第一象限内，取决于顶点位置）；若顶点在x轴下方，还可能穿过第三、四象限。

当a<0时，抛物线开口向下，可能穿过第三、四象限（或仅在第三象限内），若顶点在x轴上方，还可能穿过第一、二象限。

3. 指数函数与对数函数

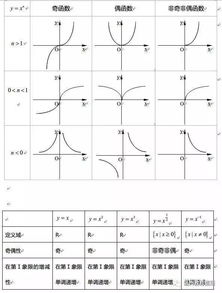
指数函数（如y=a^x，a>0且a≠1）的图像在a>1时，始终在第一、二象限；在0

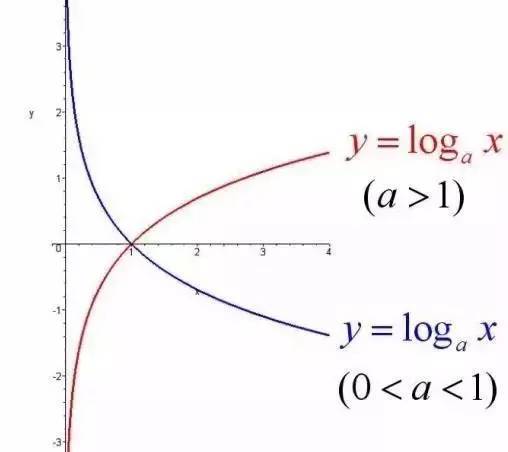
对数函数（如y=log_a(x)，a>0且a≠1）的图像在a>1时，始终在第一、四象限；在0