揭秘数学奇迹：韦达定理公式，解开多项式根之迷的钥匙！

在数学的世界里，隐藏着许多令人着迷的定律与公式，它们如同一把把钥匙，解锁着自然与宇宙的奥秘。今天，我们要深入探索的，便是一个既古老又充满智慧的定理——韦达定理，它不仅揭示了一元二次方程中根与系数之间的神秘联系，更是数学史上的一颗璀璨明珠。

韦达定理：解开方程的钥匙

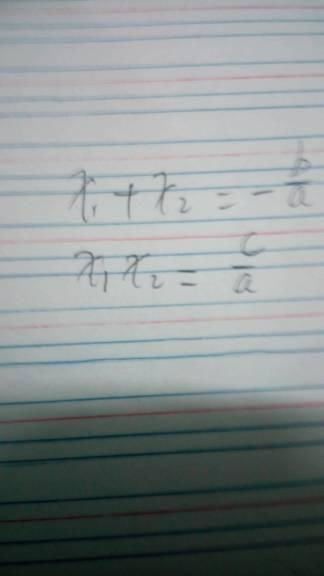
想象一下，你手中握着一个看似简单的二次方程`ax² + bx + c = 0`（其中a, b ∈ R，且a ≠ 0），它就像是一个锁定的宝箱，里面藏着两个未知数x1和x2，等待着被发现。而韦达定理，正是那把能够轻松打开这个宝箱的钥匙。它告诉我们，无需繁琐的计算，仅凭方程的系数a、b、c，就能直接得知这两个未知数之和与积的奥秘。

神奇的等式：两根之和与两根之积

韦达定理的核心，可以用两个简洁而深刻的等式来表达：

两根之和：`x1 + x2 = -b/a`

两根之积：`x1 * x2 = c/a`

这两个等式，如同魔法般地将原本隐藏在复杂方程背后的根与系数之间的关系，清晰地展现在了我们眼前。无论是求解方程的根，还是分析方程的性质，韦达定理都为我们提供了一条捷径。

深入剖析：韦达定理的无限魅力

然而，韦达定理的魅力远不止于此。通过对这两个基本等式的进一步推导，我们还可以得到更多有趣且实用的结论。比如：

根的平方和：`x1² + x2² = (x1 + x2)² - 2x1x2 = (-b/a)：²` -1 /2x(1c²/ +a )`1

/-x 2倒²数的 =平方 (和x1² + x2²)/(x1²x2²) = [(-b/a)² - 2(c/a)] / (c/a)²`

三次方的和：`x1³ + x2³ = (x1 + x2)(x1² - x1x2 + x2²) = -b/a * [(b/a)² - 3c/a]`

这些变形公式，如同韦达定理的衍生品，它们在代数、方程求解、函数分析等领域都有着广泛的应用。韦达定理，就像是一个源头，滋养着数学的各个领域，让数学的世界更加丰富多彩。

韦达定理的实战应用

理论虽好，但若不能应用于实际，便如同空中楼阁。韦达定理在解决实际问题时，同样展现出了其独特的优势。无论是物理中的运动学问题，还是经济学中的增长模型，甚至是日常生活中的一些简单计算，韦达定理都能为我们提供有力的支持。

比如，在解决某些物理问题时，我们可能需要求解一个关于速度的二次方程。利用韦达定理，我们可以直接得出两个速度解之和与积，进而分析物体的运动状态。在经济学中，韦达定理也可以帮助我们分析市场供需关系的变化对价格的影响。

韦达定理的启示：数学之美

韦达定理的存在，不仅仅是一个数学定理那么简单。它更像是一扇窗，让我们得以窥见数学之美。在韦达定理的背后，是数学家们对自然规律的深刻洞察和不懈追求。他们用简洁的公式和等式，揭示了自然界中复杂而美妙的联系。

同时，韦达定理也教会了我们一种思维方式：在面对复杂问题时，不妨从更高的视角去审视它，寻找那些隐藏在表面之下的简单规律。正如韦达定理所揭示的那样，即使是一个看似复杂的二次方程，其背后也隐藏着如此简洁而深刻的联系。

结语：探索数学的无限可能

在数学的海洋里，韦达定理只是众多宝藏之一。但正是这些宝藏的存在，激发了我们对未知世界的无限好奇和探索欲。让我们带着对数学的热爱和敬畏之心，继续在这片浩瀚的海洋中遨游吧！也许在不久的将来，你会发现更多属于你的数学之美。

通过本文的介绍，相信你已经对韦达定理有了更深入的了解和认识。不妨在下次遇到二次方程时，试着用韦达定理去解开它的秘密吧！你会发现，数学的世界比你想象的更加精彩和迷人。