在数学的广阔天地里,扇形,这一独特的几何形状,以其优雅的形态和丰富的应用,成为了连接平面几何与现实生活的重要桥梁。扇形,顾名思义,是圆的一部分,由两条半径和它们之间的弧所围成的图形。它不仅在视觉上给人以美感,更在面积计算上展现出其独特的数学魅力。提到扇形的面积公式,虽然通常我们所说的“三个”可能稍有误解(因为严格来说,扇形面积的主要计算公式仅一个,但可以通过不同角度理解和推导),但我们可以从公式的本质、推导过程、应用实例以及与其他几何知识的联系等多个维度,来深入探索这一公式的奥秘。

扇形面积公式,最直接且常用的表达形式是:$$S = \frac{1}{2}lr$$,其中$S$代表扇形面积,$l$是扇形的弧长,$r$是扇形的半径。这个公式简洁而深刻,它揭示了扇形面积与其弧长和半径之间的直接关系。通过这一公式,我们可以轻松计算出任意给定弧长和半径的扇形面积,无需复杂的图形分割或面积叠加。
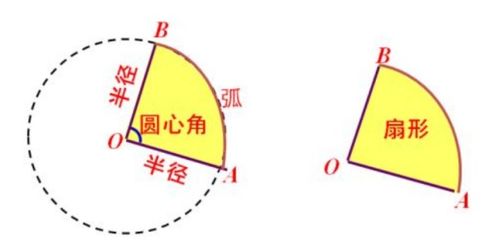
想象一个完整的圆,其面积为$\pi r^2$。如果我们将这个圆均等地切成若干个扇形,并将其中一个扇形展开,它会近似于一个等腰三角形(当扇形很小或分割很细时,这种近似更加精确)。这个三角形的底即为扇形的弧长$l$,高则为圆的半径$r$。因此,扇形的面积可以近似看作这个三角形的面积,即$\frac{1}{2} \times \text{底} \times \text{高} = \frac{1}{2}lr$。

从另一个角度来看,扇形的面积也可以通过极限的概念来推导。考虑圆上的一个小角度$\theta$(以弧度为单位)对应的扇形,其弧长可以表示为$\theta r$(弧长公式)。随着$\theta$的减小,这个扇形越来越接近一个小的等腰三角形,其面积趋近于$\frac{1}{2} \theta r^2$(这里利用了三角形面积的另一种表达形式,但需要注意这里的$\theta$需转换为与三角形高相关的角度或进行适当变换)。然而,更准确的做法是直接利用扇形的定义和弧长公式,结合圆的面积公式,通过极限的思想证明$\frac{1}{2}lr$的正确性。这涉及到微积分中的极限理论和面积积分的基本概念。
扇形面积公式的应用远远超出了纯粹的数学计算范畴,它在众多领域都有着重要的实践意义。
工程设计:在建筑、桥梁、机械等工程设计中,扇形结构因其稳定性和美观性而常被采用。设计师需要利用扇形面积公式来精确计算所需材料的量,以确保设计的经济性和安全性。
地理测绘:在地图制作和地理测绘中,扇形区域常用于表示特定方向上的距离范围或影响区域。通过扇形面积公式,可以估算出这些区域的大致面积,为地理分析提供基础数据。
经济学:在经济学中,扇形图作为一种数据可视化工具,常用于展示各类比例关系。虽然这里的“扇形”更多是象征意义上的,但理解扇形面积的概念有助于我们更好地解读和分析这些数据图表。
日常生活:从扇子的设计制作到蛋糕的切片分配,扇形面积的计算都在无形中影响着我们的日常生活。
扇形面积公式不仅是一个独立的数学工具,它还与许多其他几何概念和公式紧密相连。
圆的面积:扇形是圆的一部分,因此扇形的面积与整个圆的面积之间存在直接的比例关系。这个比例由扇形的圆心角占整个圆周角的比例决定。
三角形面积:如前所述,通过特定的视角和近似方法,扇形面积可以与三角形的面积建立联系。这种联系加深了我们对几何图形之间内在关系的理解。
比例与相似:在解决与扇形相关的问题时,比例和相似的概念往往成为关键。例如,两个相似的扇形之间,其面积之比等于对应边(即半径和弧长)之比的平方。
综上所述,扇形面积公式虽看似简单,实则蕴含着丰富的数学思想和广泛的应用价值。通过多维度地探索其本质、推导过程、应用实例以及与其他几何知识的联系,我们不仅能够更深刻地理解这一公式,还能在解决实际问题时灵活运用所学知识,展现出数学的无穷魅力。
63.93M阳光趣爱
48.53M号令天下手机版
97.06Martand艺术社交平台
17.46M大管家巡航系统
20.27M速漫库app安卓版
0B西西漫画去广告版
93.25M速看短剧2026
39.98M快对作业2026最新版
40.36M饭团探书旧版本大全
18.50M这就是警察手游安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2