数学中cot的定义及常见应用方法

在数学的世界里，存在着许多基础而重要的概念，它们如同构建知识大厦的砖石，每一块都承载着特定的意义与用途。其中，“cot”这一术语，尽管可能不如加减乘除那般广为人知，但在三角函数的殿堂里，它却扮演着举足轻重的角色。本文旨在探讨“cot”在数学中的确切含义，以及它的一般应用方式，带领读者走进这个微妙而精妙的数学领域。

数学中的cot：定义与起源

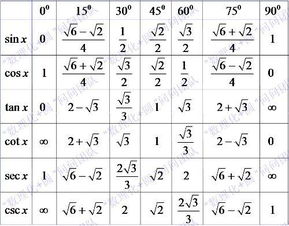
在数学特别是三角函数中，“cot”是“cotangent”（余切）的缩写，代表了一个特定的角度关系。具体来说，对于任意角θ（通常在直角三角形中考虑，或在单位圆上通过坐标来定义），cotθ定义为该角的相邻边长度与对边长度之比，即cotθ = 相邻边/对边。这个定义与正弦（sinθ = 对边/斜边）和余弦（cosθ = 相邻边/斜边）紧密相关，但有着自己独特的表达方式和应用场景。

余切函数cotθ的性质深受其定义影响，它在θ趋近于0°或180°（或π/2弧度）时趋于无穷大或不存在（数学上称为“未定义”），因为这些角度下对边长度趋于0，而相邻边长度保持有限。这一特性使得余切函数在特定问题求解时具有独特的价值。

一般用法与应用场景

1. 三角函数计算

最直接的应用莫过于在解决涉及三角函数的计算问题中。当问题中直接给出了角度θ及其相邻边和对边长度的具体值，或者需要求解这些值时，余切函数cotθ便成为了一个有力的工具。通过设定cotθ等于给定或待求的比例，可以轻松地建立方程并求解相关问题。

2. 三角恒等式与变换

在三角恒等式的学习和应用中，cot函数也频繁出现。它与其他三角函数（如sin、cos、tan等）之间存在着紧密的转换关系，如cotθ = 1/tanθ = cosθ/sinθ。这些关系不仅加深了我们对三角函数之间内在联系的理解，还为复杂三角表达式的化简提供了可能。例如，在解决涉及多个三角函数的复杂方程时，合理利用cot与其他函数的转换关系，可以大大简化计算过程。

3. 几何问题

在解决几何问题时，尤其是那些涉及直角三角形或需要利用三角函数进行测量的场景中，cot函数同样发挥着重要作用。例如，在建筑设计中，确定屋顶的倾斜角度或计算桥梁支撑结构的稳定性时，往往需要利用cot函数来计算相关边长或角度。此外，在航海、天文学等领域，cot函数也常被用于计算视线与水平线之间的夹角等。

4. 物理学与工程学应用

尽管cot函数在数学上的定义和应用看似抽象，但它在实际的物理学和工程学问题中同样具有广泛的应用。例如，在力学中分析斜面的摩擦力、在电路学中计算阻抗角（虽然通常使用复数表示法，但本质上涉及到了三角函数的应用）、在信号处理中分析波形的相位差等，都可能直接或间接地涉及到cot函数的使用。

结语

综上所述，cot作为数学中三角函数的一员，虽然在日常对话中可能不如其他基础数学概念那样频繁提及，但在解决特定类型的问题时，它却展现出了不可替代的作用。从简单的三角函数计算到复杂的几何、物理及工程学问题，cot函数以其独特的定义和性质，为我们提供了一种强有力的数学工具。通过深入理解和灵活应用cot函数，我们能够更加精准地描述和解析自然界及工程实践中的各种现象和问题，进一步拓展数学的应用领域和深度。