在探索数学的广袤疆域时,我们不可避免地会遇到一系列看似悖离日常经验却又深刻影响科学进步的概念,其中,“虚数”便是这一领域里一颗璀璨的明珠。虚数,这个听起来或许带有几分神秘与不确定性的名词,实则构成了数学大厦中不可或缺的基石,它不仅在纯数学领域占据重要地位,更在物理学、工程学等多个学科中展现出其独特的魅力和实用价值。
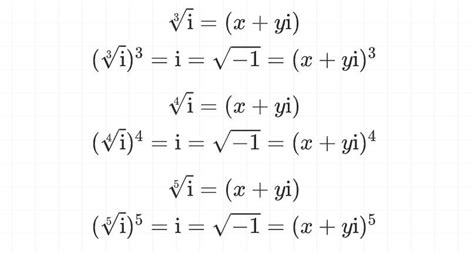
故事的开始,要追溯到16世纪,当时欧洲的数学家们正沉浸在解决代数方程的狂热之中。意大利数学家吉罗拉莫·卡尔达诺,在解决三次方程时,首次遭遇了这样一个困境:方程的解中包含了一个他前所未见的“数”,这个数既不是正数也不是负数,它不能代表任何实际长度的线段,也无法在数轴上找到对应的位置。这个数,就是后来我们所称的“虚数”。卡尔达诺虽然意识到了它的存在,但由于时代的局限和观念的束缚,他选择了隐瞒这一发现,只将其记录在自己的私人笔记中,直到多年后才被另一位数学家拉斐尔·邦贝利公开。

为了更系统地描述这类特殊的数,数学家们引入了一个全新的符号——i(或称为虚数单位),并定义它为满足方程i² = -1的数。这个看似简单的定义,却彻底颠覆了人们对数的传统认知。在此之前,所有的数(实数)都可以通过加、减、乘、除等基本运算得到,并且这些运算的结果仍然保持在实数域内。而虚数的出现,则标志着数学世界向一个全新的维度扩展,它允许我们构建出那些在传统实数运算中无法直接得到的数,即复数。复数由实部和虚部组成,一般形式为a + bi,其中a和b为实数,i为虚数单位。

尽管虚数在最初被发现时因其“虚无缥缈”的特性而备受争议,但随着时间的推移,人们逐渐认识到虚数在数学乃至科学领域的巨大价值。在几何学中,复数可以与平面上的点一一对应,这使得复数成为了描述二维空间变换的强有力工具。在物理学中,虚数更是无处不在,它们在量子力学、电磁学、声学等领域中扮演着关键角色。例如,在量子力学中,波函数作为描述粒子状态的数学工具,就经常包含复数;而在电磁学中,利用复数可以简化交流电路的分析过程,使得复杂的电路问题变得清晰明了。

1. 电路分析:在交流电路中,电压和电流往往随时间作周期性变化,这种变化可以用复数来表示。通过复数的运算,可以方便地求解电路的阻抗、功率等参数,大大简化了计算过程。
2. 信号处理:在信号处理领域,复数被广泛应用于表示和分析信号的频谱特性。通过傅里叶变换,可以将时域中的信号转换到频域中进行分析,而频域中的信号则常常以复数的形式表示。
3. 量子力学:量子力学是描述微观粒子行为的理论框架,其中波函数是关键概念之一。波函数一般为复数形式,它包含了粒子状态的所有信息。通过复数运算,可以求解粒子的能量、动量等物理量,进而揭示微观世界的奥秘。
4. 控制理论:在自动控制系统中,复数的应用同样广泛。通过引入复频率的概念,可以将系统的动态特性在复平面上直观地表示出来,进而分析系统的稳定性和性能。
综上所述,虚数作为数学中一个独特的概念,不仅丰富了数的家族成员,更在多个学科领域中展现出其强大的应用潜力。从最初的抽象概念到如今广泛而深入的应用实践,虚数的发展历程见证了人类智慧的不断进步和对未知世界的勇敢探索。在未来的科学研究中,我们有理由相信,虚数将继续发挥其独特的作用,引领我们向更加深邃和广阔的知识领域迈进。
 山海经幻想录安卓版类型:网络游戏
山海经幻想录安卓版类型:网络游戏山海经幻想录安卓版简介 《山海经幻想录》安卓版是一款基于中...
 puffin浏览器app官方正版类型:实用工具
puffin浏览器app官方正版类型:实用工具Puffin 浏览器是一款专为移动设备优化的高速浏览器,以其...
 Lime记账类型:实用工具
Lime记账类型:实用工具Lime记账是一款专为个人和家庭设计的简洁高效的记账应用,旨...
 斩妖诀游戏类型:角色扮演
斩妖诀游戏类型:角色扮演《斩妖诀》是一款融合了古典神话与现代RPG元素的冒险游戏。玩...
 舞力全开2026手机控制器类型:卡牌游戏
舞力全开2026手机控制器类型:卡牌游戏《舞力全开2026》是一款结合音乐与舞蹈的健身娱乐游戏,旨在...
67.18M有朋
86.44M咒术回战:幻影游行2026最新版
42.96M澜湄视听
79.76M猫耳FM官方最新版
37.59M爱漫画app官方最新版
76.84M换游官方版
105.77M欢友
56.25M游击队鲍勃
72.94MGMOD躲猫猫联机版
116.18M爆炸街道游戏
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2