一立方,这个看似简单的数学单位,在日常生活中却扮演着举足轻重的角色。无论是在建筑、工程、物理还是数学领域,一立方的概念都无处不在。那么,一立方究竟是怎么算的呢?本文将从多个角度深入探讨这个问题,帮助大家更好地理解一立方的计算方法和应用。
首先,我们需要明确一立方的定义。在数学中,一立方指的是一个边长为1单位的正方体的体积。这个单位可以是米、厘米、毫米等,具体取决于我们所使用的度量衡系统。例如,如果我们说的是一立方米(m³),那么它就是一个边长为1米的正方体的体积。同样地,一立方厘米(cm³)就是一个边长为1厘米的正方体的体积。

要计算一个正方体的体积,我们只需要将其边长的三次方计算出来即可。这是因为正方体的体积公式是V = a³,其中V表示体积,a表示边长。所以,一立方的计算就是1的三次方,即1³ = 1。这个结果虽然简单,但它却构成了我们理解和计算更复杂体积的基础。

接下来,我们来看一看一立方在实际应用中的例子。在建筑和工程领域,一立方经常用来表示材料的用量。比如,当我们说需要一立方米的沙子来填充某个空间时,我们指的就是需要一个边长为1米的正方体沙子那么多。同样地,在物理和化学实验中,一立方也经常被用来表示气体的体积或者液体的容量。
除了正方体,一立方还可以作为其他形状体积计算的参考。比如,对于圆柱体,我们可以通过计算其底面积和高度的乘积来得到体积。如果圆柱体的底面是一个圆形,那么底面积就是π乘以半径的平方。对于球体,其体积公式是(4/3)πr³,其中r是球的半径。虽然这些形状的体积计算公式比一立方的计算要复杂得多,但它们都是基于类似的几何原理得出的。
在实际应用中,我们经常会遇到需要计算不规则形状体积的情况。这时,我们可以通过将不规则形状分解成若干个规则形状的组合来进行计算。比如,一个不规则的石头可以通过将其近似看作一个长方体、圆柱体或者多个这样的形状的组合来进行体积估算。当然,这种方法的准确性取决于我们分解和近似的精度。
除了体积计算,一立方还与密度、质量等物理量密切相关。密度是指单位体积内物质的质量,它的计算公式是ρ = m/V,其中ρ表示密度,m表示质量,V表示体积。如果我们知道某种物质的密度和一立方的体积,那么我们就可以计算出这种物质在一立方内的质量。反过来,如果我们知道某种物质的质量和一立方的体积,那么我们也可以计算出这种物质的密度。
在环保和能源领域,一立方的概念同样重要。比如,在测量空气中的污染物浓度时,我们通常会以每立方米空气中的污染物含量来表示。同样地,在评估某个区域的能源消耗时,我们也可能会以每立方米空间内的能源消耗量作为指标。这些应用都充分说明了一立方在日常生活中的重要性和实用性。
此外,一立方还与我们的生活品质息息相关。比如,在住宅设计中,合理的空间布局和体积规划可以提高居住舒适度。如果房间的体积过大而家具和装饰物过少,就会显得空旷而冷清;反之,如果房间的体积过小而家具和装饰物过多,就会显得拥挤而压抑。因此,在设计住宅时,我们需要根据实际需求来合理规划房间的体积和布局。
在农业领域,一立方的概念也经常被用到。比如,在灌溉系统中,我们需要根据农作物的生长需求和土壤的含水量来合理控制灌溉量。这时,我们就可以通过计算每立方米土壤中的水分含量来指导灌溉工作。同样地,在肥料施用方面,我们也可以根据每立方米土壤中的养分含量来确定肥料的种类和施用量。
随着科技的发展,一立方的应用也在不断拓展。比如,在3D打印技术中,我们可以通过精确控制材料的体积和形状来制造出各种复杂的产品。在虚拟现实技术中,我们也可以通过构建三维模型来模拟真实世界中的场景和物体。这些技术的背后都离不开对体积的精确计算和控制。
综上所述,一立方作为一个简单而重要的数学单位,在日常生活和各个领域中都有着广泛的应用。它不仅是我们理解和计算体积的基础,还与密度、质量等物理量密切相关;同时,它也与我们的生活品质、农业生产以及科技发展紧密相连。因此,我们应该深入了解和掌握一立方的计算方法和应用,以便更好地应对各种实际问题和挑战。
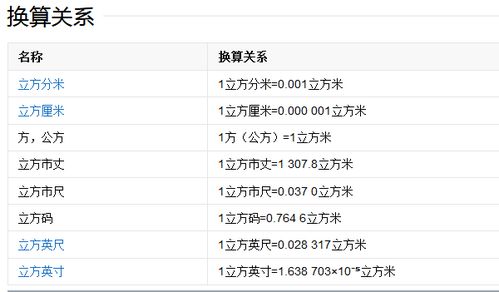
当然,在计算体积时,我们还需要注意单位的换算和精度的控制。不同的单位之间可能存在换算关系,比如1立方米等于1000立方分米或者1000000立方厘米。在进行单位换算时,我们需要确保计算结果的准确性。同时,在实际应用中,由于各种因素的影响(如测量误差、材料变形等),我们可能需要对计算结果进行修正和调整。因此,在进行体积计算时,我们需要保持谨慎和细致的态度,以确保结果的准确性和可靠性。
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2