CNM排列组合公式详解

在我们日常生活中，无论是从选择早餐吃什么，还是到规划一场活动的参与者，排列组合的概念无处不在。当我们面对需要从多个选项中选择一部分，并且关心这些选择的不同顺序或不考虑顺序时，排列组合公式就派上了用场。其中，“cnm排列组合公式”是一个非常重要的工具，它能帮助我们计算这些选择的数量。接下来，我们就来详细了解一下这个公式的各个方面，让它变得通俗易懂。

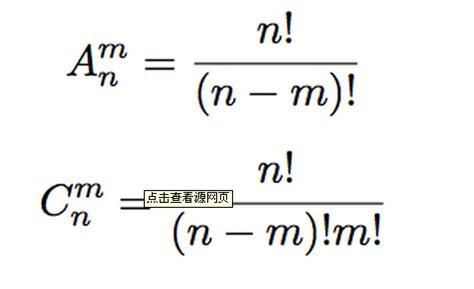
首先，我们需要明确什么是排列和组合。简单来说，排列就是按照一定的顺序选择元素，而组合则是不考虑顺序的选择。举个例子，假设有三个不同的苹果（A、B、C），我们要选择两个来吃。如果选择的是A和B，那么在排列中，AB和BA是两个不同的结果，因为顺序不同；而在组合中，AB和BA被视为同一种结果，因为我们只关心选择了哪两个苹果，而不关心它们的顺序。

接下来，我们进入正题，详细讲解“cnm排列组合公式”。

一、组合公式（Cnm）

组合公式，记作C(n, m)，表示从n个不同元素中选出m个元素的所有组合的个数。它的计算公式是：

C(n, m) = n! / [m!(n - m)!]

这里，“!””表示阶乘，即一个数与它前面所有正整数的乘积。例如，5! = 5 × 4 × 3 × 2 × 1 = 120。

组合公式背后的逻辑是：首先，我们考虑从n个元素中选择m个元素的所有可能排列，这有n!种情况。但是，每一种排列中，m个被选中的元素自身又有m!种排列方式，这些是我们不需要区分的。同时，剩下的n-m个未被选中的元素也有(n-m)!种排列方式，这些同样是我们不需要关心的。因此，为了得到真正的组合数，我们需要从n!中除以m!和(n-m)!，以消除这些多余的排列。

二、排列公式（Anm）

虽然题目主要询问的是组合公式，但为了全面理解，我们也简要介绍一下排列公式。排列公式，记作A(n, m)，表示从n个不同元素中选出m个元素的所有排列的个数。它的计算公式是：

A(n, m) = n! / (n - m)!

排列公式的逻辑相对简单：从n个元素中选择m个元素进行排列，对于第一个位置有n种选择，对于第二个位置有n-1种选择（因为已经选走了一个），以此类推，直到最后一个位置有n-m+1种选择。因此，总的排列数为n × (n-1) × ... × (n-m+1)，这正是n! / (n-m)!。

三、cnm排列组合公式的应用场景

了解了公式之后，我们来看看这些公式在实际中的应用场景。

1. 抽奖活动

假设有一个抽奖活动，从100名参与者中随机抽取5名幸运观众。我们需要计算有多少种不同的中奖组合。这就是一个典型的组合问题，因为中奖者的顺序并不重要。所以，我们可以使用组合公式C(100, 5)来计算。

2. 球队阵容

假设一支足球队需要从23名球员中选择11名首发球员。但是，首发球员的位置（如前锋、中场、后卫）是固定的，因此我们需要考虑排列。这就是一个排列问题，因为除了选择球员外，还需要确定他们的位置。所以，我们可以使用排列公式A(23, 11)来计算所有可能的首发阵容（虽然在实际中，由于位置和角色的限制，并不是所有排列都是合理的，但这个公式给了我们一个理论上的上限）。

3. 菜品搭配

假设一家餐厅提供5种主菜和3种甜点，顾客需要从中选择一道主菜和一道甜点。我们需要计算有多少种不同的搭配方式。这同样是一个组合问题，因为顾客的选择顺序并不重要（先选主菜还是先选甜点是一样的）。所以，我们可以使用组合公式C(5+3, 1)（这里我们将主菜和甜点视为一个整体，从中选择1个，即选择一道主菜或一道甜点，但因为两者是独立的，所以实际上应该是C(5, 1) × C(3, 1)种组合，但为了简化说明，我们用了C(5+3, 1)来类比说明组合的思路）。不过更准确的计算方式是考虑两者的组合，即5 × 3种搭配。

四、如何使用计算器或编程语言计算组合数

虽然理解公式很重要，但在实际应用中，我们可能更倾向于使用计算器或编程语言来快速计算结果。

使用计算器

许多现代计算器都内置了组合和排列的计算功能。通常，这些功能可以通过特定的按键序列来访问。例如，在一些计算器上，你可能需要先按下“组合”或“排列”的按键，然后输入n和m的值，最后按下“=”来得到结果。

使用编程语言

在编程语言中，计算组合数通常可以通过数学库或自定义函数来实现。例如，在Python中，你可以使用`math.comb(n, m)`函数来计算组合数（注意：这个函数在Python 3.8及更高版本中可用）。如果你使用的是较旧的Python版本，你可以自己编写一个函数来实现组合数的计算。

五、总结

通过本文的介绍，我们了解了“cnm排列组合公式”是什么，以及它是如何计算的。我们还探讨了组合和排列的区别，以及这些公式在实际生活中的应用场景。希望这些信息能够帮助你更好地理解和应用排列组合公式，从而解决生活中的各种问题。无论是在选择早餐、规划活动还是进行数据分析时，掌握这个工具都将使你的决策更加准确和高效。