等腰三角形,这一几何图形中的瑰宝,因其独特的对称性和简洁美,长久以来吸引着无数数学爱好者和学习者的目光。在等腰三角形的众多性质中,“三线合一”无疑是最为引人入胜且富有教育意义的一条。那么,等腰三角形的“三线合一”究竟指的是哪三线呢?它们之间又有着怎样的奇妙关系呢?让我们一起踏上这段探索之旅。
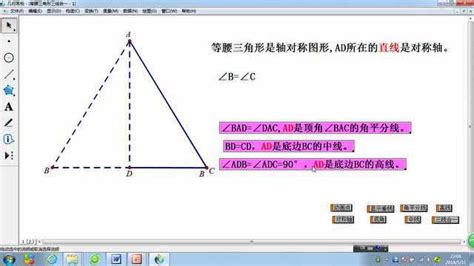
等腰三角形,顾名思义,就是两边长度相等的三角形。设等腰三角形为ABC,其中AB=AC,那么顶点A就是等腰三角形的顶角顶点,而底边BC上的任意一点D(不与B、C重合),都有可能成为我们探讨“三线合一”的起点。

首先,我们来看第一条线——中线。在三角形中,中线是连接一个顶点和它所对边的中点的线段。在等腰三角形ABC中,若D是底边BC的中点,那么线段AD就是等腰三角形的中线。中线的一个基本性质是它将对边平分,即BD=CD。在等腰三角形中,中线还承担着保持三角形对称性的重任,因为AD的存在使得三角形在垂直于BC的方向上呈现出完美的对称性。

接下来,我们探讨第二条线——高线。在三角形中,高线是从一个顶点垂直于它所对边(或其延长线)的线段。在等腰三角形ABC中,若D是底边BC上(或其延长线上)的任意一点,且AD垂直于BC,那么线段AD就是等腰三角形的高线。高线的一个重要性质是它使得三角形的面积可以方便地通过底和高来计算。在等腰三角形中,高线还扮演着揭示顶角大小的角色,因为顶角A的大小与AD的长度和BC的长度之比有关。

最后,我们来认识第三条线——角平分线。在三角形中,角平分线是将一个角平分为两个相等的角的线段,且这个线段是这个角的对边的内角的平分线。在等腰三角形ABC中,角平分线AD将顶角A平分为两个相等的角BAD和CAD。角平分线的一个显著性质是它将对边(或其延长线)上的某一点到两个顶点的距离相等,即BD上的点到A和B的距离等于CD上的点到A和C的距离(在特定情况下)。在等腰三角形中,角平分线进一步强化了三角形的对称性,因为它不仅平分了顶角,还使得三角形的两部分在角平分线的方向上呈现出对称。

现在,我们已经认识了等腰三角形的三条重要线段:中线、高线和角平分线。那么,“三线合一”的奇妙之处又在哪里呢?
在等腰三角形中,一个令人惊叹的事实是:当底边上的点D恰好是底边的中点时,中线AD、高线AD和角平分线AD会重合为同一条线段!这就是等腰三角形的“三线合一”性质。这一性质不仅揭示了等腰三角形在几何上的高度对称性,还为我们在解决与等腰三角形相关的问题时提供了极大的便利。
例如,当我们需要证明等腰三角形中的某个角是直角时,可以利用“三线合一”性质来构造高线,并证明它与底边垂直;当我们需要求解等腰三角形的面积时,可以利用中线来找到底边的中点,并通过高线来计算面积;而当我们需要证明等腰三角形中的两个角相等时,可以利用角平分线来简化证明过程。
此外,“三线合一”性质还为我们在学习更复杂的几何知识和解决更难的几何问题时提供了基础。例如,在探究直角三角形的性质时,我们可以将等腰直角三角形看作是一个特殊的等腰三角形,并利用“三线合一”性质来简化对直角边和斜边的关系的理解;在解决三角形的相似和全等问题时,“三线合一”性质也可以作为我们证明三角形相似或全等的有力工具。
值得注意的是,“三线合一”性质并不仅仅适用于等腰三角形。在一些特殊的三角形中,如等边三角形(三边都相等的三角形),这一性质同样适用。在等边三角形中,任意一边上的中线、高线和角平分线都会重合为同一条线段,从而进一步体现了等边三角形在几何上的完美对称性。
然而,尽管“三线合一”性质在几何学中有着广泛的应用和深刻的内涵,但我们在学习和应用它时也需要注意一些细节。例如,在构造等腰三角形的高线时,需要确保高线与底边垂直;在利用中线求解面积时,需要准确找到底边的中点;在利用角平分线证明两个角相等时,需要确保角平分线确实将角平分为两个相等的部分。
总之,“三线合一”是等腰三角形中一个既简单又深刻的性质。它不仅揭示了等腰三角形在几何上的高度对称性,还为我们在解决与等腰三角形相关的问题时提供了极大的便利。通过深入理解和灵活应用这一性质,我们可以更好地掌握几何学的知识和方法,从而在数学学习的道路上走得更远。
在探索等腰三角形的“三线合一”性质的过程中,我们不仅领略了数学的简洁美和对称性美,还学会了如何将抽象的数学概念和性质转化为解决实际问题的有力工具。这种从具体到抽象、再从抽象到具体的学习过程,不仅锻炼了我们的思维能力和解决问题的能力,还让我们在数学的海洋中感受到了无穷的乐趣和魅力。因此,让我们继续深入探索数学的奥秘吧!
76.40M我狙打得贼准2
320.35M五羊本田最新版
28.04M地狱把妹王正版
26.21M好看电视手机版
17.19M蓝莓影院免费版
15.77M3d漫画免费阅读漫画
49.57M花店改头换面
55.21M改头换面幻想
23.35M养成制服女友手游安卓版
47.78Mthe L
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2