在几何学中,平行四边形是一种基本的四边形形状,具有两组对边平行且等长的特点。对于平行四边形的面积计算,我们主要依赖于一个简单而实用的公式。掌握这一公式,不仅能帮助我们快速解决与平行四边形面积相关的问题,还能在更深层次上理解几何图形的面积计算方法。
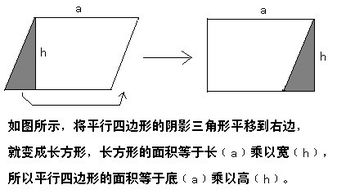
平行四边形的面积公式为:面积 = 底 × 高。这里的“底”通常指的是平行四边形的一组对边中的任意一条,而“高”则是从这条底边出发,垂直于底边并且连接平行四边形另一组对边的线段。这个公式简单明了,但在实际应用中,我们需要注意如何准确地找到并测量底和高。

在平行四边形中,由于两组对边平行且等长,我们可以选择任意一组对边作为底边。同时,高也是唯一的,即从底边出发的唯一一条垂直于底边的线段。在计算面积时,确保底和高的正确选择至关重要。如果我们选择了错误的底或高,或者没有正确理解垂直的概念,都可能导致面积计算错误。
为了更深入地理解平行四边形的面积公式,我们可以将其与矩形的面积公式进行比较。矩形的面积也是底乘以高,但矩形的两组对边都是垂直的。平行四边形则可以看作是由矩形经过一定角度的旋转得到的。因此,平行四边形的面积计算公式与矩形相似,但需要注意底和高的选择以及它们之间的垂直关系。
在解决实际问题时,我们可能会遇到各种形状的平行四边形。有些平行四边形的底和高可能很容易找到,而有些则可能需要通过一些几何变换或辅助线来确定。例如,当平行四边形的底边在水平位置时,我们可以直接测量底和高的长度。但当底边倾斜时,我们可能需要通过作垂线或构造辅助三角形来找到高。
此外,平行四边形的面积公式还可以与其他几何知识相结合,解决更复杂的问题。例如,我们可以利用平行四边形的面积公式来计算与它相关的三角形的面积。如果一个三角形与一个平行四边形等底等高,那么三角形的面积就是平行四边形面积的一半。这个性质可以帮助我们快速找到与平行四边形相关的三角形的面积。
除了基本的面积计算外,平行四边形的面积公式还可以应用于更广泛的领域。例如,在建筑设计中,我们可能需要计算一个平行四边形形状的窗户或门的面积。在物理学中,平行四边形面积的概念也可以用于计算力或电场等物理量在某一方向上的分量。此外,在计算机图形学和游戏开发中,平行四边形的面积公式也是重要的基础知识之一。
为了更好地理解和应用平行四边形的面积公式,我们可以通过一些具体的例子来进行练习。例如,假设我们有一个平行四边形,其底边长度为10厘米,高为6厘米。根据面积公式,我们可以计算出这个平行四边形的面积为60平方厘米。同样地,如果我们知道一个平行四边形的面积和底边长度,我们也可以求出它的高。
此外,我们还可以通过构造不同的平行四边形来进一步探索面积公式的应用。例如,我们可以构造一个等腰梯形,然后将其拆分为一个矩形和两个等腰直角三角形。通过计算矩形和两个三角形的面积之和,我们可以验证等腰梯形的面积公式是否与平行四边形的面积公式一致。这种练习不仅可以帮助我们巩固知识,还可以培养我们的几何思维和解决问题的能力。
需要注意的是,在应用平行四边形的面积公式时,我们需要确保所给的图形确实是平行四边形。如果图形不是平行四边形,或者底和高没有正确选择,那么面积公式将不适用。因此,在解决问题之前,我们需要先对图形进行仔细的观察和分析,确保它满足平行四边形的定义和性质。
总之,平行四边形的面积公式是几何学中的基础知识之一。通过掌握这个公式,我们可以快速计算平行四边形的面积,并解决与之相关的各种问题。同时,我们还可以通过与其他几何知识的结合和应用,进一步拓展平行四边形面积公式的应用范围。无论是在学习、工作还是生活中,掌握平行四边形的面积公式都将对我们有所帮助。
为了加强理解和记忆,我们可以多做一些与平行四边形面积相关的练习题。这些练习题可以包括直接计算面积的问题,也可以包括需要通过几何变换或辅助线来确定底和高的问题。通过不断的练习和实践,我们可以更加熟练地掌握平行四边形的面积公式,并在实际应用中取得更好的效果。同时,我们还可以尝试将平行四边形的面积公式与其他几何知识相结合,解决更复杂的问题,进一步提升我们的几何思维和解决问题的能力。
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2