几何平均值如何表示？

在数学的广阔领域中，几何平均值作为一种重要的统计量，扮演着不可或缺的角色。它不仅在数学理论中占据一席之地，还在物理学、经济学、工程学等多个领域有着广泛的应用。本文将从几何平均值的定义、计算方法、性质特征、实际应用以及与其他平均值的对比等多个维度，全面而深入地探讨几何平均值。

一、几何平均值的定义

几何平均值，简称几何均数，是对一组正实数进行乘积运算后，再取n次方根得到的值。若有一组正实数a1, a2, ..., an，则这组数的几何平均值G可以通过以下公式计算：

G = (a1 * a2 * ... * an)^(1/n)

这个定义直观地揭示了几何平均值的本质——它反映了这组数在几何尺度上的平均水平。换句话说，几何平均值是衡量一组数在乘法运算下的中心位置的一种统计量。

二、几何平均值的计算方法

计算几何平均值的过程相对简单，但需要注意的是，所有参与计算的数都必须是正实数。具体步骤如下：

1. 乘积运算：首先，将这组数全部相乘，得到一个乘积。

2. 开方运算：然后，将这个乘积开n次方，n是这组数的个数。

例如，对于一组数2, 4, 8，其几何平均值为：

G = (2 * 4 * 8)^(1/3) = 4

值得注意的是，当这组数中包含0或负数时，几何平均值是无法定义的，因为0或负数无法参与乘法运算或开方运算。

三、几何平均值的性质特征

几何平均值作为一种特殊的平均值，具有一系列独特的性质特征：

1. 正数性：几何平均值总是大于0（当且仅当所有数都大于0时）。这一性质确保了它在许多实际问题中的适用性。

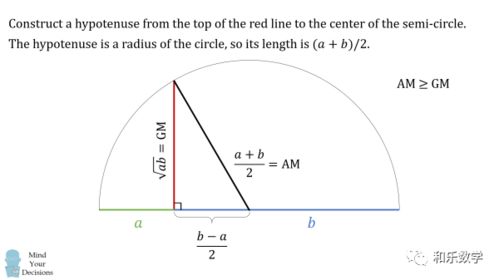
2. 不等式关系：对于任意一组正实数，其几何平均值总是小于或等于其算术平均值（算术平均值即这组数的和除以数的个数）。这一不等式关系在数学上被称为均值不等式，是几何平均值的一个重要性质。

3. 乘法不变性：如果一组数中的每个数都乘以一个相同的正实数k，那么新的几何平均值将是原几何平均值的k倍。这一性质反映了几何平均值在乘法运算下的稳定性。

4. 受极端值影响较小：与算术平均值相比，几何平均值对极端值（特别大或特别小的数）的敏感性较低。这意味着，当一组数中存在极端值时，几何平均值更能反映这组数的整体平均水平。

四、几何平均值的实际应用

几何平均值在多个领域都有着广泛的应用，以下是一些典型的例子：

1. 物理学：在物理学中，几何平均值常用于描述物理量的平均变化。例如，在声学领域，声音强度的几何平均值用于描述多个声源共同作用下的平均声音强度。

2. 经济学：在经济学中，几何平均值常用于计算复利下的平均增长率。例如，在计算股票或债券的年平均收益率时，使用几何平均值可以更准确地反映实际收益情况。

3. 工程学：在工程学中，几何平均值常用于描述几何形状的平均尺寸。例如，在机械设计中，轴的直径、管道的截面尺寸等都可以使用几何平均值来进行优化。

4. 生物学：在生物学中，几何平均值常用于描述生物体的生长速度或繁殖率。例如，在种群生态学中，使用几何平均值可以预测种群数量的变化趋势。

五、几何平均值与其他平均值的对比

为了更全面地理解几何平均值，我们需要将其与其他常见的平均值进行对比：

1. 算术平均值：算术平均值是最直观、最常用的平均值。它通过将一组数的和除以数的个数来得到。与几何平均值相比，算术平均值对极端值更加敏感，因此在处理包含极端值的数据时可能不够准确。

2. 调和平均值：调和平均值是另一种常见的平均值。它通过将一组数的倒数之和的倒数来得到。调和平均值常用于处理速度、时间等倒数关系的物理量。与几何平均值相比，调和平均值的应用范围相对较窄。

3. 加权平均值：加权平均值是一种更灵活的平均值。它根据每个数的重要性（即权重）来计算平均值。加权平均值在多个领域都有广泛的应用，包括统计学、经济学、社会学等。与几何平均值相比，加权平均值在处理具有不同重要性的数据时更具优势。

六、结语

综上所述，几何平均值作为一种重要的统计量，在数学理论和实际应用中都发挥着不可或缺的作用。它不仅具有独特的性质特征，还在物理学、经济学、工程学等多个领域有着广泛的应用。通过与其他平均值的对比，我们可以更全面地理解几何平均值的优势和局限性。在未来的学习和研究中，我们应该更加深入地探讨几何平均值的性质和应用，以充分发挥其在解决实际问题中的潜力。同时，我们也应该注意到，任何统计量都有其适用范围和局限性，因此在选择和使用统计量时应该根据实际情况进行权衡和选择。