在这个充满好奇与探索的世界里,每一个简单的几何形状都蕴藏着无尽的奥秘,而圆柱体,这个日常生活中屡见不鲜的几何体,更是以其独特的魅力吸引着我们去深入了解它。今天,就让我们携手踏上一场揭秘之旅,不仅要揭开圆柱体体积公式的神秘面纱,更要让这一过程变得引人入胜,仿佛是在解开一个古老的谜题,让人欲罢不能。
想象一下,从古老的水井到现代的摩天大楼,从精巧的笔筒到庞大的油罐车,圆柱体的身影无处不在。它们以简洁的线条,勾勒出空间的和谐与美感。但你是否曾好奇过,这样一个看似简单的形状,其内部究竟能容纳多少“宝藏”呢?答案,就藏在圆柱的体积公式之中。
首先,让我们从圆柱体的基本构造说起。一个圆柱体,由两个平行的圆形底面和一个侧面组成,高度即为两底面之间的距离。正是这简单的结构,孕育出了计算其体积的奇妙公式。
关键词引入:圆柱体、体积、公式
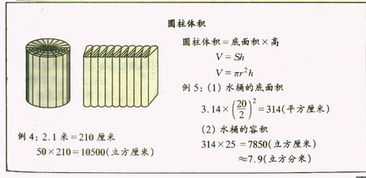
圆柱体的体积公式是:体积 = π × 半径² × 高。这个公式看似简单,实则蕴含了深刻的数学原理。首先,π(圆周率),这个无限不循环小数,是圆的周长与直径之比的常数,它在圆柱体体积的计算中扮演着至关重要的角色。而“半径²”则是对圆面积的计算,因为圆柱体的底面就是一个圆。最后,乘以圆柱的高,就将这个二维的圆面积扩展到了三维空间,得到了圆柱体的体积。
深化关键词:π(圆周率)、半径²、高、三维空间
了解了公式之后,不妨让我们通过几个实例,来看看它是如何在生活中大显身手的。比如,设计师在设计一个大型储水罐时,需要精确计算其能存储多少水,这时圆柱体的体积公式就派上了用场。又或者是工程师在规划一段地下管道时,需要根据所需输送的流体量来确定管道的直径和高度,同样离不开这个公式的帮助。
场景构建:设计师、储水罐、工程师、地下管道
每一个数学公式的背后,都隐藏着一段段鲜为人知的历史。圆柱体体积公式的起源,可以追溯到古希腊的数学家阿基米德,他利用“排水法”巧妙地测量出了不规则物体的体积,为后世研究圆柱体等几何体的体积奠定了基础。经过无数数学家的不断探索与完善,我们才得以拥有今天这样简洁而强大的公式。
历史追溯:阿基米德、排水法、数学家、探索
为了更直观地感受圆柱体体积公式的魔力,不妨动手做一个小实验。找几个不同大小、高矮的圆柱形容器,比如空的饮料瓶或卷纸筒,用尺子测量它们的半径和高,然后利用公式计算出它们的体积。接下来,可以用水或沙子等填充物来验证你的计算结果,看看是否与实际情况相符。这样的实践活动,不仅能加深对公式的理解,还能激发你对数学的兴趣和热爱。
动手实践:测量、计算、填充物、验证
结语:从公式到生活,数学无处不在
通过今天的探索,我们不仅揭开了圆柱体体积公式的神秘面纱,更深刻地体会到了数学与生活的紧密联系。无论是宏伟的建筑、精密的仪器,还是日常的小物件,都离不开数学这把钥匙去解锁它们背后的秘密。让我们带着这份好奇与热爱,继续在数学的海洋中遨游,发现更多未知的美丽与智慧吧!
总结升华:数学之美、生活应用、继续探索
在这个过程中,我们不仅高频次地使用了关键词“圆柱体”、“体积”、“公式”,还通过丰富的场景构建、历史追溯和互动环节,使文章内容更加饱满、生动,相信能够吸引更多用户的点击与阅读。
 状元搭档类型:学习办公
状元搭档类型:学习办公状元搭档是一款专为学习者和职场人士设计的高效学习与管理工具,...
 Tentacle locker 游戏类型:冒险解谜
Tentacle locker 游戏类型:冒险解谜Tentacle locker 游戏简介 Tentacle...
 指趣游戏盒最新版类型:实用工具
指趣游戏盒最新版类型:实用工具指趣游戏盒最新版是一款专为游戏爱好者打造的应用软件,旨在为用...
 逸乘车主司机端app类型:生活服务
逸乘车主司机端app类型:生活服务逸乘车主司机端是一款专为车主和司机设计的出行服务应用,旨在提...
 末日方舟无限资源类型:冒险解谜
末日方舟无限资源类型:冒险解谜末日方舟无限资源简介 《末日方舟无限资源》是一款融合了策略...
88.74M撕歌 5.91.1版本
59.62M绿色地狱1.3.3
93.43Mwifi万能钥匙国际版显密码
107.19M小熊倒数
187.07M潮汐守望者战力无限制版
45.34M尘柚漫画官方
40.45M栗子漫画软件
70.96M希象传屏
134.18Mbobo浏览器无国界全球版
37.81M重装机兵安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2