在数学的浩瀚宇宙中,隐藏着许多令人着迷的概念和定理,它们如同璀璨星辰,点亮了人类智慧的夜空。今天,我们要探索的是一个既基础又充满魅力的数学名词——互质数。你或许听说过它,但你真的了解互质数的奥秘吗?让我们一起揭开互质数的神秘面纱,走进这个充满趣味与挑战的数学世界。
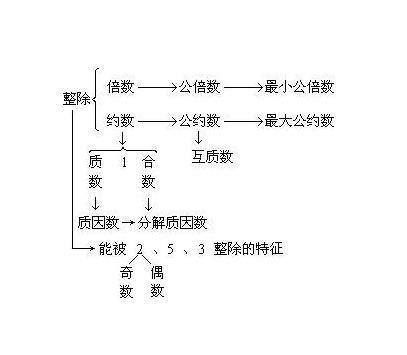
想象一下,你手中有两张数字卡片,它们分别代表两个不同的自然数。现在,请你尝试找出这两个数之间的一种特殊关系——它们是否互质?那么,什么是互质数呢?简单来说,互质数就是两个或多个整数共有的唯一正因数只有1的数。换句话说,如果两个数之间除了1以外没有其他公共因数,那么这两个数就是互质的。
听起来有些抽象?别担心,让我们通过一个简单的例子来理解。假设你手中的两张卡片上分别写着6和9,这两个数看起来似乎很普通,但如果你尝试找出它们的公共因数,你会发现除了1以外,3也是它们的公共因数。因此,6和9不是互质数。然而,如果你将其中一张卡片上的数字改为8,那么6和8之间就只有1这一个公共因数了。所以,6和8是互质数。
互质数的概念在数学中扮演着举足轻重的角色。它不仅是数学理论的基础之一,还在密码学、计算机科学、工程学等多个领域发挥着重要作用。比如,在密码学中,互质数常被用于生成公钥和私钥对,确保信息传输的安全性。在计算机科学中,互质数则被用于设计高效的算法和数据结构,提高计算机的运行效率。在工程学中,互质数的概念则有助于解决一些复杂的物理问题和优化设计方案。
那么,如何判断两个数是否互质呢?有几种常用的方法可以帮助我们快速找到答案。第一种方法是使用质因数分解法。首先,我们需要将两个数分别进行质因数分解,然后观察它们的质因数是否完全相同。如果两个数的质因数完全不同或者只有部分相同但互不影响(即不存在相同的质因数且它们的幂次也不同),那么这两个数就是互质的。例如,对于14和15这两个数,它们的质因数分解分别为2×7和3×5,由于它们的质因数完全不同,所以14和15是互质数。
第二种方法是使用辗转相除法(也称为欧几里得算法)。这种方法通过反复取余数的方式,最终可以得到两个数的最大公约数(GCD)。如果两个数的最大公约数为1,那么这两个数就是互质的。辗转相除法不仅简单易懂,而且计算效率极高,是判断两个数是否互质的首选方法之一。
除了以上两种方法外,还有一些其他的方法可以判断两个数是否互质。比如,我们可以利用整数的性质进行推导和证明;或者利用一些特殊的数学定理和公式来简化计算过程。无论采用哪种方法,关键在于理解和掌握互质数的本质特征及其在数学中的应用。
在深入了解互质数的过程中,你可能会发现一些有趣的数学现象和规律。比如,对于任意两个相邻的自然数(除了0和1以外),它们都是互质的。这是因为相邻的自然数之间不可能存在其他的公共因数(除了1以外)。另外,对于任意一个素数p和任意一个不等于p的整数q(q不为0),p和q也都是互质的。这是因为素数只有1和它本身两个因数,所以不可能与其他整数存在其他的公共因数。
互质数的概念还与一些数学难题密切相关。比如,哥德巴赫猜想就是一个著名的数学难题之一。它提出:任意一个大于2的偶数都可以表示为两个素数之和。虽然这个猜想至今仍未被证明或反驳,但许多数学家认为它与互质数的性质有着密切的联系。如果哥德巴赫猜想成立的话,那么任意两个大于2的偶数都可以看作是互质的两个素数之和(因为素数之间只有1这一个公共因数)。这将进一步加深我们对互质数的理解和认识。
当然,互质数的应用远不止于此。在日常生活和工作中,我们经常会遇到需要判断两个数是否互质的情况。比如,在设计密码时,我们需要确保生成的密钥对是互质的,以保证密码的安全性;在编程中,我们需要利用互质数的性质来优化算法和数据结构;在物理学和工程学中,我们也需要借助互质数的概念来解决一些复杂的问题和设计方案。
总之,互质数是一个既简单又深刻的数学概念。它不仅在数学理论中占据着重要的地位,还在各个领域发挥着广泛的应用价值。通过深入学习和理解互质数的性质和应用,我们可以更好地掌握数学这门学科的本质和精髓,从而在数学的世界中畅游得更远、更宽广。
现在,你已经对互质数有了更深入的了解和认识。下次当你遇到需要判断两个数是否互质的情况时,不妨尝试一下上述的方法,看看能否快速准确地找到答案。相信在探索数学的过程中,你会不断发现新的乐趣和挑战,不断激发你对数学的好奇心和求知欲。让我们一起在数学的世界中继续前行吧!
75.38M图片压缩助手app
188.63M斑马英语网课免费
61.10M春风好剧app官方正版
56.77M三林影视电视盒子
58.99M三林影视去广告版
40.05M真幻想三国志
62.87M剧满分TV版
152.92M死亡突围僵尸战争游戏手机版
15.22M腕能漫画安卓版
45.31M吞噬星空黎明安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2