实数定义揭秘：究竟何为实数？0是否包含在内？

探索实数的奥秘：它究竟是什么？0在其中扮演着怎样的角色？

在数学的世界里，实数是一个极其重要且广泛使用的概念。它几乎渗透到了我们生活的方方面面，从简单的加减乘除到复杂的科学计算，实数都扮演着不可或缺的角色。那么，实数究竟是什么？它包含了我们熟知的数字0吗？让我们一同揭开实数的神秘面纱。

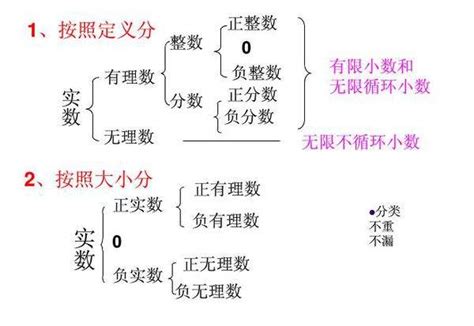
首先，让我们来明确一下实数的定义。实数，简单来说，是可以在数轴上表示出来的数。这些数包括了我们通常所说的有理数和无理数两大类。有理数，就是可以表示为两个整数之比的数，如整数、分数等。而无理数，则无法表示为两个整数的比，但它们同样可以在数轴上找到对应的位置，如π（圆周率）、e（自然对数的底数）等。实数集合就是由有理数和无理数共同构成的，它涵盖了我们在日常生活中所能接触到的几乎所有数字。

那么，0在这个实数集合中占据着怎样的位置呢？答案是肯定的，0是实数的一部分。事实上，0不仅是一个有理数（因为它可以表示为0/1或任何非零整数与0的比），而且它在数学中还具有极其重要的地位。0是数轴上的原点，是所有正负数的分界点。在运算中，0作为加数和被加数、减数和差、乘数和积、被除数和商时，都有独特的性质。比如，任何数加上0都等于它本身；任何数乘以0都等于0；0除以任何非零数都等于0，但0不能作为除数。这些性质使得0在实数体系中显得尤为特殊和重要。

接下来，让我们进一步探讨实数的一些基本性质和运算规律。首先，实数具有封闭性。这意味着在实数范围内进行加、减、乘、除（除数不为0）等运算时，其结果仍然是实数。这一性质保证了实数体系在运算中的完整性和一致性。其次，实数具有有序性。在实数轴上，我们可以根据数的大小顺序进行排列和比较。这种有序性使得我们能够进行大小的判断和不等式的求解。此外，实数还具有稠密性。在任意两个不相等的实数之间，都存在无数个其他的实数。这一性质保证了实数体系在数量上的丰富性和连续性。

在实数的运算中，有一些基本的运算法则和性质是需要我们掌握的。比如，加法和乘法的交换律和结合律、分配律等。这些运算法则和性质是实数运算的基础和保障。同时，我们还需要注意一些特殊的运算情况，如0和1在运算中的特殊性质、负数的运算规则等。

除了基本的运算外，实数还涉及到一些重要的概念和定理。比如，实数的绝对值表示一个数在数轴上与原点的距离；实数的平方根和立方根分别表示一个数的平方和立方等于另一个数时的解；实数的近似数和有效数字则涉及到实数的精度和舍入误差等问题。此外，实数体系中还有一些重要的定理和性质，如实数系的连续性定理（也称为实数系的完备性定理）、介值定理、单调有界定理等。这些定理和性质为我们研究和解决实数问题提供了有力的工具和方法。

那么，学习实数对我们有什么实际意义呢？首先，实数是数学和科学中的基础概念之一。掌握实数的概念和运算规律对于我们学习更高级的数学知识、解决复杂的科学问题都是至关重要的。其次，实数在日常生活和工作中也有着广泛的应用。比如，在金融领域，我们需要利用实数进行货币的计算和比较；在工程领域，我们需要利用实数进行尺寸的测量和计算；在计算机科学领域，我们需要利用实数进行数据的存储和处理等。因此，学习和掌握实数的概念和运算规律对于我们提高个人素质、适应社会发展都具有重要的意义。

最后，让我们来总结一下本文的主要内容。实数是在数轴上可以表示出来的数，包括有理数和无理数两大类。0是实数的一部分，具有特殊的地位和性质。实数具有封闭性、有序性和稠密性等基本性质，并涉及到一些重要的概念和定理。学习和掌握实数的概念和运算规律对于我们学习数学知识、解决科学问题以及适应社会发展都具有重要的意义。

希望通过本文的介绍，大家能够对实数的概念和性质有一个更加全面和深入的了解。同时，也希望大家能够认识到学习实数的重要性和实际意义，积极投入到实数的学习和实践中去。相信在不久的将来，大家一定能够在数学和科学领域取得更加优异的成绩和成就！