在数学的浩瀚宇宙中,隐藏着无数令人着迷的公式与定理,它们如同璀璨星辰,照亮了人类智慧的道路。而在这片星河之中,“雅可比行列式”无疑是一颗耀眼夺目的明珠,它以其独特的魅力和广泛的应用领域,吸引着无数探索者的目光。今天,就让我们一同揭开雅可比行列式的神秘面纱,感受它所带来的数学之美与实用之力。
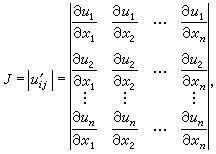
在数学的世界里,函数变换是连接不同空间、解决复杂问题的桥梁。而雅可比行列式,正是这座桥梁上的一把金钥匙,它揭示了多元函数在变换过程中体积或面积的变化规律。简单来说,雅可比行列式是衡量一个多元函数在某一点处,如何将输入空间的微小体积或面积映射到输出空间的量度。这个量度不仅在数学理论上具有重要地位,更在实际应用中发挥着举足轻重的作用。

雅可比行列式,记作J,是对于一个向量值函数f(x,y,...,z) = (u(x,y,...,z), v(x,y,...,z), ..., w(x,y,...,z)),在点(x,y,...,z)处,其各个偏导数构成的矩阵的行列式。这个定义听起来或许有些抽象,但正是这样的定义,使得雅可比行列式能够精确地描述函数在不同空间之间的“扭曲”程度。

想象一下,你手中有一张二维的地图,现在你想知道,当这张地图被某个函数“拉伸”或“压缩”后,地图上的面积会发生怎样的变化?雅可比行列式正是解答这个问题的关键。在二维情况下,它告诉我们,一个微小的矩形区域在函数作用下,会变成一个怎样的平行四边形,并且这个平行四边形的面积与原始矩形面积的比值,就是雅可比行列式的值。同样的道理,在三维甚至更高维度中,雅可比行列式也能告诉我们体积的变化情况。

在微积分中,链式法则是求解复合函数导数的重要工具。而雅可比行列式,可以被视为链式法则在多元函数变换中的延伸。它允许我们计算一个复合函数在不同坐标系下的导数,从而解决更为复杂的积分、微分问题。这种能力,使得雅可比行列式成为许多数学分支中的关键工具,如微分几何、偏微分方程等。
在物理学、工程学等领域,经常需要进行坐标变换,如从直角坐标系到极坐标系、从笛卡尔坐标系到球坐标系等。雅可比行列式在这些变换中发挥着至关重要的作用。它不仅帮助我们计算变换后的面积或体积,还能确保在变换过程中物理量的守恒性,如质量、能量等。
在概率论和统计学中,随机变量的变换是一个常见的问题。雅可比行列式可以帮助我们计算变换后随机变量的概率密度函数,从而进行更为精确的概率分析和统计推断。这种能力,使得雅可比行列式成为数据分析、机器学习等领域中的重要工具。
在图像处理和计算机视觉领域,图像的缩放、旋转、扭曲等操作是不可或缺的。这些操作本质上都是对图像像素坐标的变换。雅可比行列式能够帮助我们计算变换后的图像中,各个区域的面积变化,从而确保图像的几何一致性和视觉效果的连续性。此外,在图像配准、物体识别等任务中,雅可比行列式也扮演着重要角色。
在经济学和金融学中,我们经常需要分析不同经济变量之间的关系,以及这些关系在特定条件下的变化情况。雅可比行列式可以帮助我们计算经济模型在参数变化下的敏感度,从而预测经济行为的可能结果。此外,在金融工程中,雅可比行列式也被用于计算衍生品价格、风险管理等方面。
从数学的严谨推理到物理的直观理解,从理论的深入探索到实践的广泛应用,雅可比行列式以其独特的魅力和强大的功能,成为连接不同学科、解决复杂问题的桥梁。它不仅揭示了多元函数变换中的奥秘,更在多个领域中发挥着不可替代的作用。随着科学技术的发展,雅可比行列式的应用将会越来越广泛,它将继续引领我们探索未知、解决难题,推动人类文明的进步与发展。
在这个充满挑战与机遇的时代,让我们一同拥抱雅可比行列式所带来的数学之美与实用之力,共同开启一段探索数学奥秘的奇妙旅程。在这个过程中,我们或许会发现,数学不仅仅是一门学科,更是一种思维方式、一种看待世界的方式。而雅可比行列式,正是这样一种方式的具体体现,它让我们在纷繁复杂的世界中,找到了理解和解释现象的新视角和新方法。
146M修勾逃生巨人危机最新版
60.76M爱趣手游盒子
283.73M鸿蒙智行官方版
55.77M住房宝app
55.25M减压魔方模拟器安卓版
146.07M看图王app
97.42M果冻RPG
46.67M号令天下2026
92.58M我在阴间当差内置菜单
101.70M铲屎官
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 琼ICP备2023003481号-5