三角函数值表是数学中一个极为重要的工具,尤其在处理角度与边长关系时,它为我们提供了精确的数值参考。三角函数主要包括正弦(sin)、余弦(cos)和正切(tan),这些函数在直角三角形中定义,并且可以通过单位圆进行扩展,从而应用于任何角度。三角函数值表列出了不同角度(通常以度或弧度为单位)下这些函数的值,这些值在解决各种数学问题及工程应用中至关重要。
首先,我们需要了解三角函数的基本定义。在一个直角三角形中,假设一个角为θ,其对边为a,邻边为b,斜边为c。正弦函数sinθ定义为对边a与斜边c的比值,即sinθ=a/c;余弦函数cosθ定义为邻边b与斜边c的比值,即cosθ=b/c;正切函数tanθ则定义为对边a与邻边b的比值,即tanθ=a/b。当角度θ为锐角时,这些定义直观且易于理解。然而,当θ扩展到钝角、直角或超过直角时,就需要通过单位圆或其他方法来确定其值。

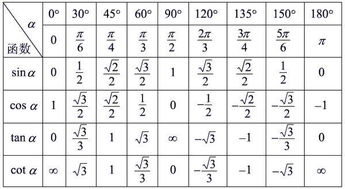
三角函数值表通常以角度为行标签,以函数值为列标签。对于每个角度,表中会列出sin、cos和tan的值。这些值可以是分数、小数或四舍五入后的近似值,具体取决于表的精度要求。在实际应用中,我们通常使用四位或更多位小数来表示这些值,以确保计算的准确性。

在三角函数值表中,一些特殊角度的值尤为重要,因为它们具有简单的表达式或易于记忆的特点。例如,0°和90°(或0弧度和π/2弧度)是两个关键的特殊角度。对于0°,sin0°=0,cos0°=1,tan0°=0/1=0;对于90°,sin90°=1,cos90°=0,tan90°则趋向于无穷大(因为此时分母b为0)。这些特殊角度的值在解决涉及三角函数的问题时经常作为参考点。

除了特殊角度外,三角函数值表还列出了其他常见角度的值,如30°、45°和60°(或π/6、π/4和π/3弧度)。这些角度在直角三角形中具有特殊的几何关系,因此它们的三角函数值也具有简单的表达式。例如,对于30°,sin30°=1/2,cos30°=√3/2,tan30°=√3/3;对于45°,sin45°=cos45°=√2/2,tan45°=1;对于60°,sin60°=√3/2,cos60°=1/2,tan60°=√3。
在实际应用中,三角函数值表的作用不仅仅局限于查找特定角度下的函数值。它还可以用于计算未知角度或边长。例如,在解决直角三角形问题时,如果我们知道其中一个角和一条边长,就可以利用三角函数值表来找出其他边长或角度。此外,三角函数值表还可以用于解决涉及周期性变化的问题,如波动、振动和旋转运动等。在这些问题中,角度通常随时间而变化,而三角函数则用于描述这种变化。
值得注意的是,三角函数值表通常只列出0°到90°(或0弧度到π/2弧度)之间的值。对于其他角度,我们可以利用三角函数的周期性和奇偶性来找到其值。例如,对于大于90°的角度,我们可以将其转换为小于90°的等效角度,并利用三角函数的奇偶性来确定其正负号。同样地,对于负角度或弧度值,我们也可以利用三角函数的周期性和奇偶性来找到其对应的正值。
此外,随着计算机技术的发展,现代数学软件和计算器已经能够直接计算任意角度下的三角函数值,而无需查阅三角函数值表。然而,了解三角函数值表的基本内容和结构仍然非常重要,因为它有助于我们理解三角函数的基本性质和周期性,以及它们在数学和物理学中的应用。
在使用三角函数值表时,我们还需要注意其精度和适用范围。不同的三角函数值表可能具有不同的精度和适用范围,因此在选择使用时需要仔细比较和选择。同时,我们还需要注意角度的单位问题。在大多数三角函数值表中,角度通常以度为单位列出,但在某些情况下,我们可能需要将其转换为弧度或其他单位才能进行计算。因此,在使用三角函数值表之前,我们需要先确定所需的角度单位和精度要求,并确保所选的表能够满足这些要求。
总的来说,三角函数值表是数学中一个非常重要的工具,它为我们提供了精确计算三角函数值的方法,并广泛应用于各种数学问题和工程应用中。虽然现代计算机技术和计算器已经能够直接计算这些值,但了解三角函数值表的基本内容和结构仍然非常重要,因为它有助于我们更好地理解三角函数的基本性质和周期性,以及它们在数学和物理学中的应用。因此,在学习和研究三角函数时,我们应该认真对待三角函数值表的学习和应用。
 牛奶画廊像素安卓游戏类型:角色扮演
牛奶画廊像素安卓游戏类型:角色扮演牛奶画廊是一款像素风格的安卓游戏,玩家将扮演一名画家,在充满...
 全民枪神边境王者2026年激活码类型:飞行射击
全民枪神边境王者2026年激活码类型:飞行射击《全民枪神边境王者2026》是一款集射击、策略与角色扮演于一...
 棕色尘埃游戏类型:角色扮演
棕色尘埃游戏类型:角色扮演《棕色尘埃》是一款结合了策略与角色扮演元素的手机游戏,玩家将...
 万籁音乐安卓版类型:影音娱乐
万籁音乐安卓版类型:影音娱乐万籁音乐安卓版是一款专为Android设备设计的音乐播放与发...
 迷你世界雨林生存类型:角色扮演
迷你世界雨林生存类型:角色扮演《迷你世界雨林生存》是一款充满冒险与挑战的生存类游戏,玩家将...
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2