在数学的奇妙世界里,有一个阶段让人既兴奋又略带挑战,那就是初中阶段。在这个阶段,学生们开始接触到一个既神秘又充满魅力的概念——函数。想象一下,当你轻轻拨动琴弦,音符跳跃而出,每一个音符都与琴弦的振动频率和长度之间存在着一种确定的关系。这种“一个变量变化,另一个变量也随之变化,且这种变化遵循一定规律”的现象,在初中数学中就被抽象为“函数”的概念。今天,就让我们一起揭开初中函数的神秘面纱,探索它背后的奥秘,看看这个函数究竟是如何成为数学学习中的一颗璀璨明珠的。
在初中数学课堂上,函数的定义或许会让你眼前一亮。简单来说,函数就是一种特殊的对应关系,它描述了两个变量之间如何相互影响。具体来说,如果存在两个变量x和y,当x在某一范围内每取一个值时,y都按照某种确定的规则有唯一确定的值与之对应,那么我们就说y是x的函数。记作:y=f(x),其中f表示对应关系,x是自变量,y是因变量。
这个定义听起来或许有些抽象,但当我们把它应用到实际问题中时,就会发现函数其实无处不在。比如,你去超市买苹果,每斤苹果的价格是固定的,那么你买的苹果的总价y就是根据你买的苹果重量x来确定的,这就是一个典型的函数关系。
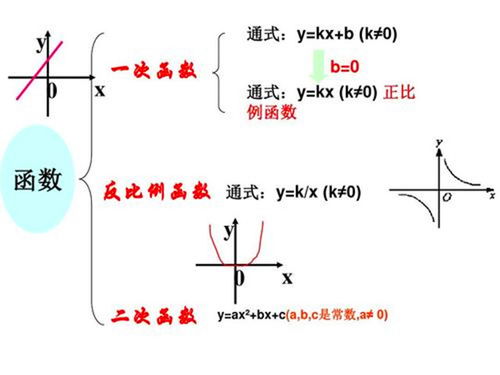
在初中数学中,函数家族成员众多,各有千秋。最常见的有线性函数、二次函数、反比例函数等,每一种函数都有其独特的魅力和应用价值。
线性函数:y=kx+b(k、b为常数,k≠0),它就像一条直线,简单而直接。无论是路程与时间的关系,还是速度与加速度的关联,线性函数都能轻松搞定。
二次函数:y=ax²+bx+c(a、b、c为常数,a≠0),它的图像是一个抛物线,优美而富有变化。无论是投篮时的抛物线轨迹,还是火箭发射时的速度变化,二次函数都扮演着重要角色。
反比例函数:y=k/x(k为常数,k≠0),它的图像是两支双曲线,神秘而迷人。在物理中的电阻、电流与电压的关系中,反比例函数更是不可或缺。
如果说函数的定义是抽象的,那么函数的图像则是直观的。在初中数学学习中,通过绘制函数的图像,我们可以更加直观地理解函数的性质。
线性函数的图像是一条直线,斜率k决定了直线的倾斜程度,截距b决定了直线与y轴的交点。通过观察直线,我们可以轻松判断函数的增减性、最值等问题。
二次函数的图像是一个抛物线,开口方向由系数a决定,顶点坐标由公式(-b/2a, f(-b/2a))给出。通过抛物线的形状,我们可以直观地看出函数的最大值或最小值,以及函数的增减性。
反比例函数的图像是两支双曲线,它们分别位于第一象限和第三象限。通过观察双曲线,我们可以发现当x增大时,y减小;当x减小时,y增大,这种反比关系正是反比例函数的魅力所在。
函数不仅存在于数学课本中,更渗透在我们的日常生活中。无论是购物时的价格计算,还是旅行时的行程规划,都离不开函数的身影。
在经济学中,成本函数、收益函数和利润函数等帮助我们分析企业的经济状况;在物理学中,运动学公式、力学公式等本身就是一种函数关系;在工程学中,建筑物的结构设计、桥梁的受力分析等也需要用到函数的知识。
此外,函数还与计算机科学紧密相连。在计算机编程中,函数是实现模块化编程的基础。通过定义和使用函数,我们可以提高代码的复用性和可读性,使编程变得更加高效和便捷。
学习函数不仅是为了掌握一种数学知识,更是为了培养我们的数学思维。通过函数的学习,我们可以学会如何抽象和概括问题,如何运用数学语言来描述和解决问题。
在解决函数问题时,我们需要运用逻辑推理、归纳演绎等数学思维方法,通过分析问题的条件、目标和约束条件,找到解决问题的途径和方法。这种思维方法的训练对于我们的未来发展具有重要意义。
同时,函数的学习还可以培养我们的创新意识和实践能力。在探索函数的过程中,我们需要不断尝试新的方法和思路,不断挑战自己的思维极限。这种勇于探索、敢于创新的精神正是我们未来成长和发展的重要支撑。
回顾初中函数的学习历程,我们不难发现,函数不仅是一个数学概念,更是一种数学思维、一种数学文化。它以其独特的魅力和广泛的应用价值,成为了数学学习中的一颗璀璨明珠。
在学习函数的过程中,我们或许会遇到困难和挑战,但正是这些困难和挑战让我们不断成长和进步。当我们掌握了函数的知识和方法后,就会发现原来
63.93M阳光趣爱
48.53M号令天下手机版
97.06Martand艺术社交平台
17.46M大管家巡航系统
20.27M速漫库app安卓版
0B西西漫画去广告版
93.25M速看短剧2026
39.98M快对作业2026最新版
40.36M饭团探书旧版本大全
18.50M这就是警察手游安卓版
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 粤ICP备2026014863号-2