三棱柱一共有多少条棱？

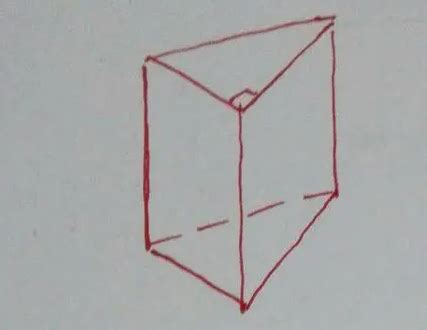
在探讨几何学的广阔领域中，三棱柱作为一个基础而重要的立体图形，其结构特性一直吸引着无数学者与爱好者的目光。三棱柱，顾名思义，是由三个矩形侧面和两个平行的三角形底面所围成的立体图形。这一简洁而富有美感的形态，不仅在日常生活中随处可见，如书籍的堆叠、建筑的结构元素等，更在几何学教育中扮演着至关重要的角色。那么，针对“三棱柱有几条棱”这一问题，我们展开一番深入的剖析与阐述。

首先，要明确的是，棱是几何学中连接两个顶点且不在同一平面上的线段。在三棱柱中，这些棱构成了其骨架，支撑着整个立体结构。为了清晰地数出三棱柱的棱数，我们可以从两个维度入手：底面和侧面。

底面的棱

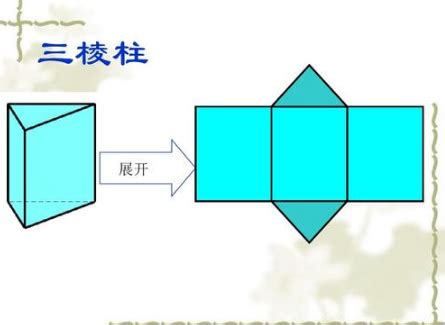
三棱柱拥有两个平行的、形状相同且大小相等的三角形底面。每个三角形底面自然拥有三条棱，这三条棱分别连接三角形的三个顶点，形成稳定的三角形结构。因此，两个底面总共包含$2 \times 3 = 6$条棱。但这仅仅是三棱柱棱数的一部分，因为三棱柱的立体性还体现在其侧面构造上。

侧面的棱

三棱柱的侧面由三个矩形组成，每个矩形都是两个底面三角形边长的延伸，形成垂直于底面的面。这些矩形侧面各自拥有四条棱，但需要注意的是，每个矩形与底面共享的那条棱（即底面三角形的边）在计算底面棱数时已经计入，所以我们在统计侧面棱数时，应避免重复计算。

具体来说，每个矩形除了与底面共享的那条棱外，还有另外三条棱是独立于底面的。由于三棱柱有三个这样的矩形侧面，因此侧面独立的棱总数为$3 \times 3 = 9$条。

综合计算

将底面的棱数与侧面的独立棱数相加，即得到三棱柱的总棱数。所以，三棱柱的棱数为$6（底面）+ 9（侧面独立棱）= 15$条。这15条棱相互连接，共同构建了三棱柱这一稳定而优雅的立体结构。

进一步理解

三棱柱的棱不仅具有数量上的特征，还蕴含着丰富的几何意义。它们不仅是构成三棱柱的基本元素，还决定了三棱柱的各种性质，如表面积、体积以及与其他立体图形的相对位置关系等。因此，在学习三棱柱时，深入理解其棱的特性显得尤为重要。

此外，三棱柱作为几何学中的一个基础模型，其棱的概念还可以推广到其他更复杂的立体图形中。比如，四棱柱（即长方体或正方体）的棱数计算就遵循类似的逻辑，只是底面的形状和侧面的数量有所不同。通过这种类比学习，我们可以更好地掌握几何学中关于立体图形棱数的一般规律。

总之，“三棱柱有几条棱”这一问题看似简单，实则蕴含了丰富的几何知识和思维方法。通过深入剖析三棱柱的棱数计算过程，我们不仅能够得到答案“三棱柱有15条棱”，更重要的是能够培养起对几何学乃至整个数学领域的浓厚兴趣和深刻理解。